2 Integers: A Quick Guide
Understanding integers is fundamental in mathematics and computer science. These numerical values, which include whole numbers and their negatives, play a crucial role in various calculations and operations. In this comprehensive guide, we will delve into the world of integers, exploring their definition, representation, and practical applications.
The Concept of Integers

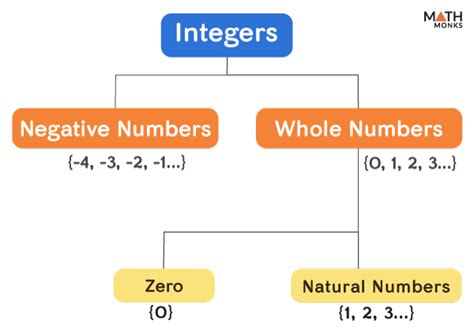
Integers are a set of numbers that comprise the positive whole numbers (1, 2, 3, …), their negatives (-1, -2, -3, …), and zero (0). They are often denoted by the symbol Z, representing the German word Zahlen, meaning “numbers.”
The significance of integers lies in their ability to represent various quantities, both positive and negative. This concept is essential in everyday life, from counting objects to measuring temperatures and even tracking financial transactions.
Representation and Notation

Integers can be represented in several ways, depending on the context and the numerical system being used. The most common notation is the decimal system, which uses the digits 0 to 9 and allows for positive and negative values.
For example, the integer 5 can be represented as a positive number, indicating a quantity of five, while -5 represents a negative quantity of five. The zero (0) is a unique integer, as it represents neither a positive nor a negative quantity, but rather the absence of a quantity.
Binary and Other Numerical Systems
In computer science and digital electronics, integers are often represented in binary form. Binary numbers use only two digits, 0 and 1, to represent all integers. This system is fundamental in computing, as it forms the basis for machine language and data storage.
Other numerical systems, such as hexadecimal (base 16) and octal (base 8), also use integers. These systems are commonly used in programming and networking, providing efficient methods for representing and manipulating large numerical values.
Operations with Integers
Integers can be manipulated through various arithmetic operations, each with its own set of rules and properties.
Addition and Subtraction
Adding and subtracting integers is straightforward. When adding two positive integers, the result is a larger positive integer. For example, 3 + 4 = 7. When subtracting a positive integer from another positive integer, the result is a smaller positive integer. For instance, 7 - 3 = 4.
With negative integers, the rules are similar. Adding two negative integers results in a larger negative integer, while subtracting a negative integer from a positive integer yields a positive integer. For example, -3 + (-4) = -7, and 7 - (-3) = 10.
Multiplication and Division
Multiplying and dividing integers follows a set of rules known as the rules of signs. When multiplying two integers with the same sign, the result is positive. Conversely, when multiplying integers with different signs, the result is negative.
For example, 4 x 5 = 20, and (-4) x (-5) = 20, while 4 x (-5) = -20. Similarly, when dividing integers with the same sign, the result is positive, and when dividing integers with different signs, the result is negative.
Other Operations
Integers can also be involved in more complex operations, such as exponentiation and logarithms. Exponentiation, represented as ab, involves raising a base number a to the power of an exponent b, where b is an integer. Logarithms, on the other hand, are the inverse of exponentiation and are used to find the exponent to which a base number must be raised to obtain a given value.
Applications of Integers
Integers have numerous applications in various fields, from mathematics and physics to computer science and engineering.
Mathematics and Physics
In mathematics, integers are fundamental in number theory, algebra, and calculus. They are used to represent quantities, perform calculations, and solve equations. In physics, integers are crucial in describing the behavior of particles, forces, and energy levels.
Computer Science and Technology
Integers are the backbone of computer science and technology. They are used in programming languages, data storage, and network communications. Integer values are essential for controlling the flow of programs, manipulating data, and performing calculations.
Everyday Life
Integers are present in our daily lives, often without us realizing it. We use integers when counting objects, tracking distances, managing finances, and even playing games. Understanding integers and their operations is crucial for making informed decisions and solving practical problems.
| Operation | Example |
|---|---|
| Addition | 3 + 4 = 7 |
| Subtraction | 7 - 3 = 4 |
| Multiplication | 4 x 5 = 20 |
| Division | 20 / 4 = 5 |
Frequently Asked Questions

What is the difference between integers and real numbers?
+Integers are a subset of real numbers. While integers include whole numbers and their negatives, real numbers also encompass rational and irrational numbers, providing a more extensive numerical range.
Can integers be used in complex calculations?
+Absolutely! Integers are fundamental in complex calculations, such as those involving matrices, vectors, and differential equations. They provide a solid foundation for more advanced mathematical concepts.
Are there any limitations to using integers in computer programming?
+While integers are widely used in programming, they do have limitations. For instance, integer variables have a maximum and minimum value, beyond which they cannot represent numbers accurately. This limitation can be overcome by using data types with larger ranges, such as long integers or floating-point numbers.



