Mastering the Multiplication Inverse: 5 Tips

The concept of multiplicative inverses, often referred to as reciprocals, is fundamental to mathematics and has wide-ranging applications. In its simplest form, a multiplicative inverse is a number that, when multiplied by the original number, results in 1. This property is a powerful tool with a rich history and numerous practical uses. Let’s delve into this mathematical concept and explore its intricacies and importance.
The Evolution of Inverses

The notion of inverses has its roots in ancient mathematical traditions, where early mathematicians grappled with the challenge of solving complex equations. Over centuries, as mathematics evolved, the understanding of inverses became more refined. The concept gained prominence during the Renaissance, as mathematicians like Leonardo da Vinci and Fibonacci explored advanced numerical concepts.
During this period, inverses played a pivotal role in understanding the behavior of numbers, and their applications extended beyond simple arithmetic. Today, multiplicative inverses are integral to fields like algebra, calculus, and number theory, offering a deep understanding of numerical relationships.
Why Multiplicative Inverses Matter

Multiplicative inverses provide a powerful tool for simplifying complex mathematical operations. By finding the inverse of a number, mathematicians can effectively ‘undo’ a multiplication operation, leading to elegant solutions for various mathematical problems. This concept is particularly useful in:
Algebraic Manipulations: In algebra, inverses are crucial for solving equations, manipulating expressions, and understanding the behavior of functions.
Calculus and Differential Equations: Inverses are vital for understanding derivatives and integrals, forming the foundation of calculus. They also play a significant role in solving differential equations.
Number Theory and Cryptography: In number theory, the study of inverses is essential for understanding the properties of numbers and their applications in cryptography, ensuring secure data transmission.
Financial and Economic Models: In finance, inverses are used to calculate interest rates, compound growth, and discount rates, providing a critical tool for economic analysis.
5 Tips for Mastering Multiplicative Inverses
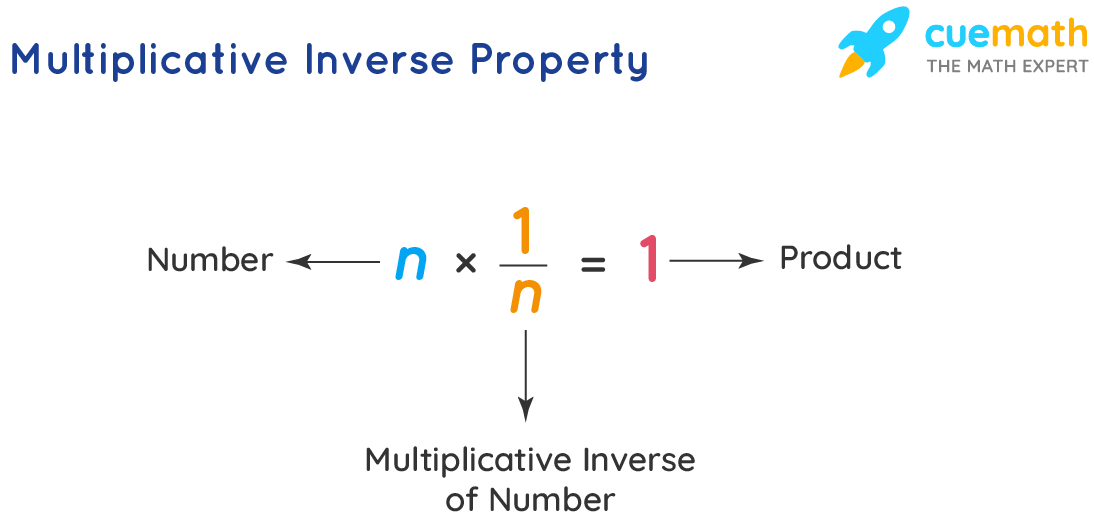
Understand the Basics: Start by grasping the fundamental definition of a multiplicative inverse. This simple concept is the foundation for all further applications. Remember, the inverse of a number ‘a’ is denoted as 1/a or a^-1, and when multiplied by ‘a’, the result is always 1.
Practice with Fractions: Working with fractions is an excellent way to reinforce your understanding of inverses. Try simplifying fractions by finding the inverse of the denominator and then multiplying it by the numerator. This practice will enhance your proficiency in manipulating fractions.
Explore Real-World Applications: Multiplicative inverses are not just theoretical concepts; they have tangible applications. Explore how inverses are used in everyday life, such as in calculating discounts, understanding interest rates, or even in cooking when measuring ingredients by their inverses (e.g., 1⁄2 cup instead of 2 cups).
Study Inverse Functions: In mathematics, the concept of inverses extends beyond numbers. Learn about inverse functions, where the output of one function becomes the input for its inverse. This understanding is crucial in fields like physics, engineering, and computer science, where functions and their inverses are used to model real-world phenomena.
Practice with Algebraic Expressions: In algebra, the ability to manipulate expressions and equations is crucial. Practice simplifying complex algebraic expressions by using inverses to cancel out terms. This skill will be invaluable when solving equations and working with more advanced mathematical concepts.
Conclusion
Multiplicative inverses are a cornerstone of mathematics, offering a powerful tool for simplifying and understanding numerical relationships. By mastering this concept, you’ll unlock a deeper understanding of mathematics and its applications. Whether you’re a student, a professional, or simply someone curious about the world of numbers, exploring multiplicative inverses will enrich your mathematical journey.
Remember, mathematics is a vast and fascinating field, and every concept, no matter how simple it may seem, has the potential to unlock new insights and applications. So, embrace the power of multiplicative inverses and let them guide you to new mathematical heights!
FAQ
What is the significance of the multiplicative inverse in number theory and cryptography?
+In number theory, multiplicative inverses play a crucial role in understanding the structure of numbers and their relationships. They are particularly important in modular arithmetic, which is the foundation of modern cryptography. In cryptography, the concept of multiplicative inverses is used to ensure secure data transmission and encryption, making it a vital tool in the digital age.
How do multiplicative inverses relate to the concept of ‘undoing’ a multiplication operation?
+Multiplicative inverses are like a mathematical ‘undo’ button for multiplication. When you multiply a number ‘a’ by its inverse 1/a, the result is always 1. This means that you can ‘undo’ the multiplication operation by multiplying the result by the inverse. This property is fundamental to solving equations and simplifying expressions.
Are there any limitations to the use of multiplicative inverses in mathematical applications?
+While multiplicative inverses are powerful, they do have limitations. For instance, not all numbers have a multiplicative inverse in the real number system. For example, the number 0 has no multiplicative inverse because any number multiplied by 0 remains 0. However, in the context of modular arithmetic, every number has a multiplicative inverse, which extends the applicability of this concept.
How can I practice applying multiplicative inverses in real-world scenarios?
+One practical way to apply multiplicative inverses is in financial calculations. For example, when calculating compound interest, you can use the inverse of the interest rate to find the discount rate. Similarly, in cooking, you can use the inverse of a measurement to simplify recipes, such as converting 1⁄4 cup to 4 cups.



