The Ultimate Guide: Synthetic Division Tips

Diving into Synthetic Division: Unlocking its Potential

Synthetic division, a powerful mathematical technique, offers an efficient approach to polynomial division. While its theoretical underpinnings are rooted in polynomial algebra, its practical applications extend far beyond. This guide aims to unravel the intricacies of synthetic division, offering a comprehensive toolkit for mastery.

Historical Evolution: From Long Division to Synthetic Simplicity

The concept of polynomial division has a rich history, with early forms of long division appearing in ancient civilizations like Egypt and Babylon. However, it was not until the 17th century that mathematicians began to explore more efficient methods, leading to the development of synthetic division.

French mathematician Abraham de Moivre, known for his work on complex numbers, is often credited with introducing the idea of synthetic division. His approach, published in the early 18th century, provided a significant breakthrough in simplifying polynomial division.

Understanding the Basics: Synthetic Division Fundamentals

At its core, synthetic division is a streamlined process that simplifies the division of polynomials. It is particularly effective for dividing a polynomial by a linear factor of the form (x - c), where c is a constant.

The key to synthetic division lies in its ability to condense the division process into a single step, eliminating the need for repetitive calculations. This efficiency makes it an invaluable tool for mathematicians, engineers, and scientists working with polynomials.

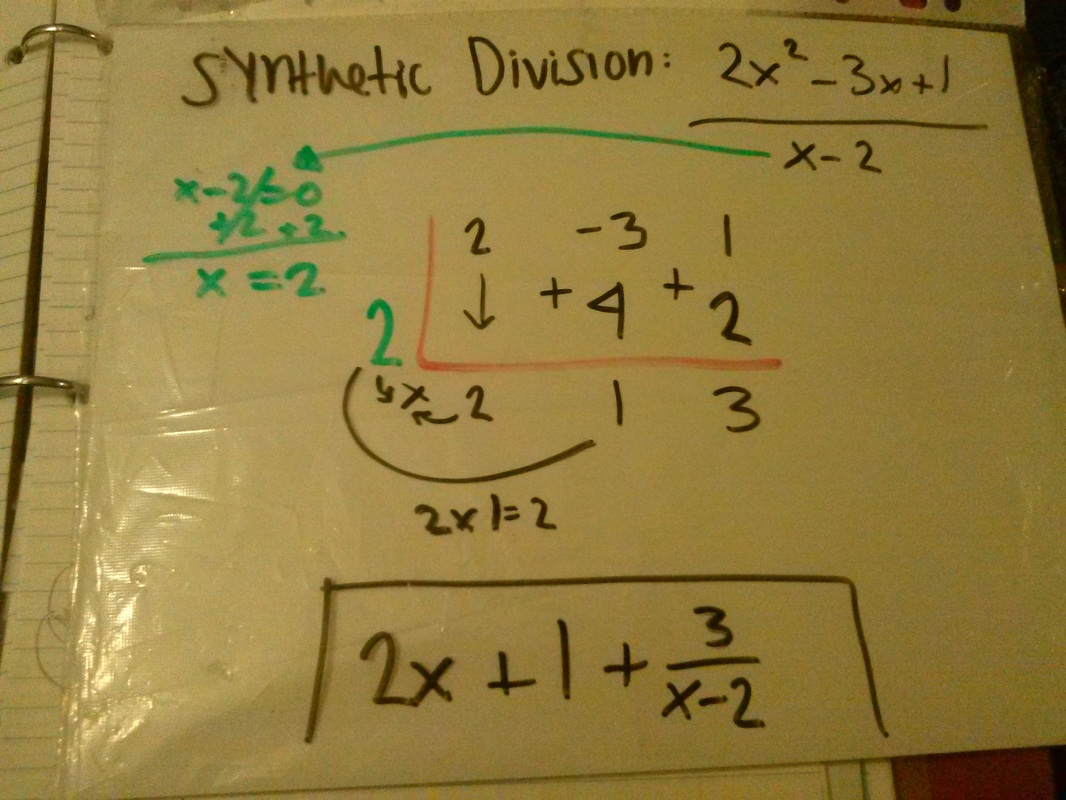
Step-by-Step Guide: Mastering Synthetic Division

To master synthetic division, follow these systematic steps:

Step 1: Prepare the Dividend Begin by arranging the coefficients of the dividend polynomial in descending order of degree. If the polynomial is in the form of a product of binomials or trinomials, factor it appropriately before proceeding.

Step 2: Construct the Synthetic Division Table Create a table with rows representing the degree of the polynomial and columns for the coefficients. The leftmost column will be for the divisor, while the remaining columns will accommodate the coefficients of the dividend.

Step 3: Perform the Division Place the divisor in the leftmost column and the first coefficient of the dividend in the second column. Now, perform the synthetic division process: - Multiply the number in the leftmost column (divisor) by the number in the second column (first coefficient). - Write the result in the row below, aligning it with the next column to the right. - Add the numbers in the third column to obtain the next coefficient. - Repeat this process until all coefficients have been used.

Step 4: Interpret the Results The numbers in the bottom row of the synthetic division table represent the coefficients of the quotient polynomial. The remainder, if any, is the last number in the bottom row.

Visualizing Synthetic Division: A Practical Example

Consider the polynomial division problem:

(3x^3 + 5x^2 - 2x + 7) / (x - 2)

Using synthetic division, we can solve this efficiently:

Step 1: Prepare the Dividend

Coefficients in descending order: 3, 5, -2, 7

Step 2: Construct the Synthetic Division Table

Degree	2	1	0
Divisor	2
Coefficients	3	5	-2	7

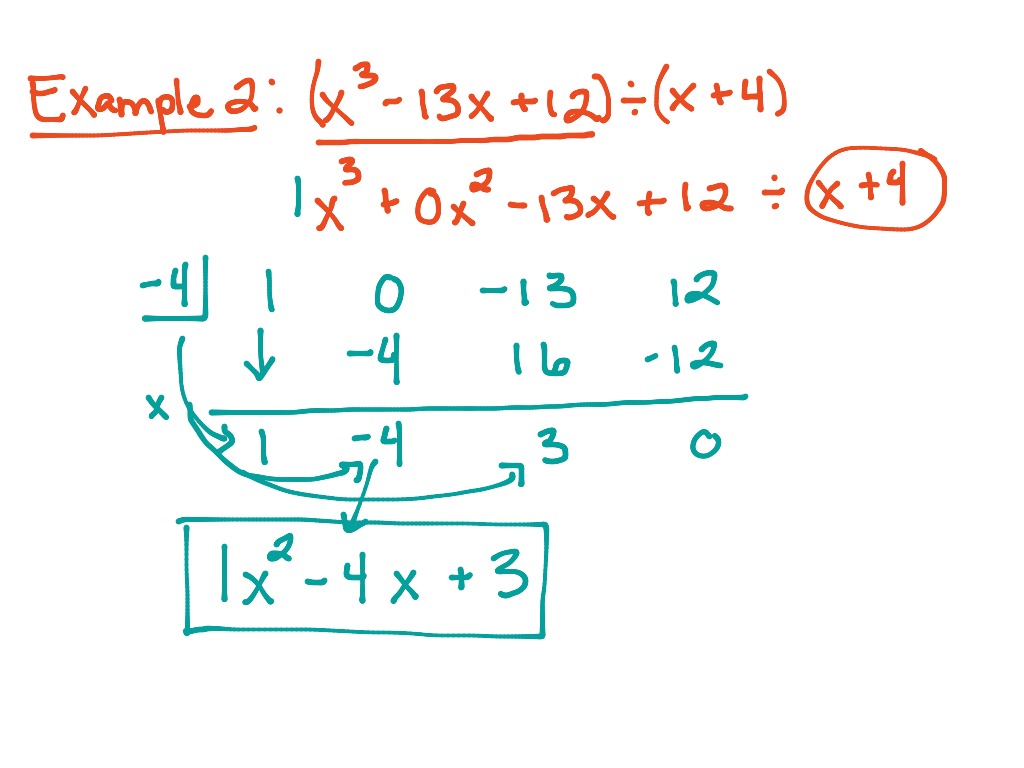
Step 3: Perform the Division

Multiplying the divisor by the first coefficient:

Degree	2	1	0
Divisor	2
Coefficients	3	5	-2	7
Product	6

Adding the coefficients:

Degree	2	1	0
Divisor	2
Coefficients	3	5	-2	7
Product	6	11

Continuing the process:

Degree	2	1	0
Divisor	2
Coefficients	3	5	-2	7
Product	6	11	-4

Step 4: Interpret the Results

The quotient polynomial is: 3x^2 + 11x - 4

The remainder is: 7

Practical Applications: Where Synthetic Division Shines

Synthetic division finds extensive applications in various fields:

Algebra: It simplifies the process of finding roots of polynomials, aiding in the solution of complex algebraic equations.

Engineering: Engineers use synthetic division to analyze signal processing systems, filter design, and control system responses.

Physics: In physics, it aids in calculating wave functions, solving differential equations, and analyzing oscillatory systems.

Computer Science: Synthetic division is integral to computer graphics, image processing, and signal analysis algorithms.

Expert Insights: Maximizing Synthetic Division’s Potential

To harness the full potential of synthetic division, consider these expert tips:

• Practice with Varied Polynomials: Synthetic division is a skill that improves with practice. Challenge yourself with polynomials of different degrees and complexities to enhance your proficiency.

• Understand the Underlying Theory: While synthetic division simplifies calculations, understanding the theoretical basis enhances your ability to apply it effectively in diverse scenarios.

• Combine with Other Techniques: Synthetic division can be a powerful tool when combined with other algebraic techniques. Explore its synergy with methods like polynomial long division or factoring to tackle more complex problems.

Conclusion: Synthetic Division’s Impact on Modern Mathematics

Synthetic division has revolutionized polynomial division, offering an efficient and streamlined approach. Its historical evolution, from ancient long division to modern synthetic simplicity, underscores its significance in the development of mathematics.

By mastering synthetic division, mathematicians, scientists, and engineers unlock a powerful tool, enhancing their problem-solving capabilities and paving the way for innovative solutions in a wide array of fields.