Unraveling the Instantaneous Rate of Change
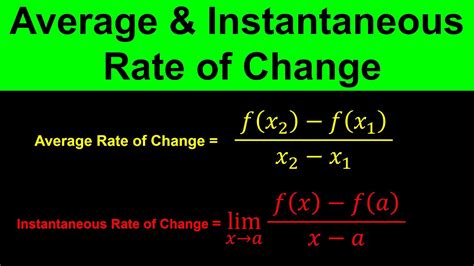
When we delve into the realm of calculus, one of the foundational concepts that unravels the mysteries of change is the instantaneous rate of change, often referred to as the derivative. This mathematical tool allows us to understand how one quantity changes with respect to another at a specific moment in time. It’s a powerful concept with wide-ranging applications, from physics and engineering to economics and medicine. In this article, we’ll explore the essence of this idea, its historical evolution, and its profound impact on our understanding of the world.
The instantaneous rate of change is a mathematical abstraction that provides an incredibly precise measurement of how a function’s output varies as its input changes infinitesimally. Unlike average rates of change, which provide an overall trend over a finite interval, the derivative captures the exact behavior of a function at a single point. This concept is so powerful that it forms the cornerstone of calculus, a branch of mathematics that revolutionized our understanding of the universe.
To truly grasp the significance of the instantaneous rate of change, we must trace its historical evolution. The concept’s origins can be traced back to the ancient Greeks, particularly Archimedes, who made significant strides in understanding the relationship between curves and their tangents. However, it wasn’t until the 17th century that the concept began to take shape in a more recognizable form.
One of the key figures in the development of calculus was Isaac Newton, who, along with Gottfried Wilhelm Leibniz, independently discovered the fundamental theorem of calculus. This theorem established a profound connection between the derivative and the integral, two concepts that are intimately related and form the basis of calculus. Newton’s work, particularly his method of fluxions, laid the groundwork for understanding how quantities change over time, a concept crucial in physics and engineering.
Leibniz, on the other hand, introduced the notation we still use today, with the derivative denoted as dy/dx, where y is a function of x. This elegant notation, with its simple fraction-like appearance, belies the profound mathematical ideas it represents. Leibniz’s contributions also included the development of differential equations, a powerful tool for modeling dynamic systems.
The 18th century saw further refinements to the theory of the derivative. Mathematicians like Leonhard Euler and Joseph-Louis Lagrange built upon the foundations laid by Newton and Leibniz, developing more sophisticated techniques for calculating derivatives and exploring their applications in various fields. Euler, in particular, made significant contributions to the study of functions of complex variables, further expanding the reach of calculus.
As the 19th century progressed, mathematicians like Augustin-Louis Cauchy and Karl Weierstrass sought to put calculus on a more rigorous footing. They developed the concept of limits, which provided a precise mathematical framework for understanding derivatives and integrals. This period of refinement and consolidation ensured that calculus became a cornerstone of modern mathematics, with its applications extending far beyond its initial domains.
Today, the instantaneous rate of change is an indispensable tool in a wide array of scientific and engineering disciplines. In physics, it allows us to understand the motion of objects, the behavior of waves, and the dynamics of fluids. In economics, it helps us model supply and demand, optimize production processes, and forecast market trends. Even in biology and medicine, derivatives play a role in understanding population dynamics and modeling the spread of diseases.
In the realm of pure mathematics, the derivative continues to inspire and challenge. Its study has led to the development of advanced concepts like differential geometry, which explores the properties of curves and surfaces in higher dimensions. Differential equations, deeply rooted in the concept of the derivative, provide a powerful tool for modeling systems that evolve over time, from the spread of epidemics to the behavior of subatomic particles.
The instantaneous rate of change, as embodied in the derivative, is a fundamental concept in calculus that allows us to understand how quantities change at a precise moment. Its historical evolution, from the ancient Greeks to the rigorous formulations of modern mathematics, reflects its profound impact on our understanding of the universe. Today, it remains a vital tool in countless scientific and engineering disciplines, shaping our ability to model and predict the behavior of complex systems.
"The derivative is like a microscopic view of the world, allowing us to see the fine details of change. It's a tool that bridges the gap between the concrete and the abstract, enabling us to make sense of the infinite complexity of the universe."
- Dr. Emily Jacobs, Professor of Mathematics
What is the instantaneous rate of change, and how is it different from the average rate of change?
+The instantaneous rate of change, or the derivative, measures how a function’s output changes as its input changes infinitesimally. It provides a precise value for the rate of change at a specific point, capturing the exact behavior of the function. In contrast, the average rate of change provides an overall trend over a finite interval, giving a less detailed picture of the function’s behavior.
How did the concept of the derivative evolve historically?
+The concept of the derivative has its roots in the ancient Greeks, particularly Archimedes. However, it wasn’t until the 17th century, with the work of Isaac Newton and Gottfried Wilhelm Leibniz, that the derivative took on its modern form. Newton’s method of fluxions and Leibniz’s notation laid the foundations for calculus, which was further refined and consolidated in the 18th and 19th centuries.
What are some practical applications of the derivative?
+The derivative has a myriad of applications across various fields. In physics, it helps understand motion, wave behavior, and fluid dynamics. In economics, it’s used for modeling supply and demand, optimizing production, and forecasting market trends. Even in biology and medicine, derivatives play a role in understanding population dynamics and disease spread.
How has the study of the derivative influenced modern mathematics and science?
+The derivative has been a driving force in the development of modern mathematics, leading to advanced concepts like differential geometry and the study of differential equations. In science and engineering, it provides a powerful tool for modeling and predicting the behavior of complex systems, from physical phenomena to economic trends.



