Mastering the Art: Solve Absolute Value Equations

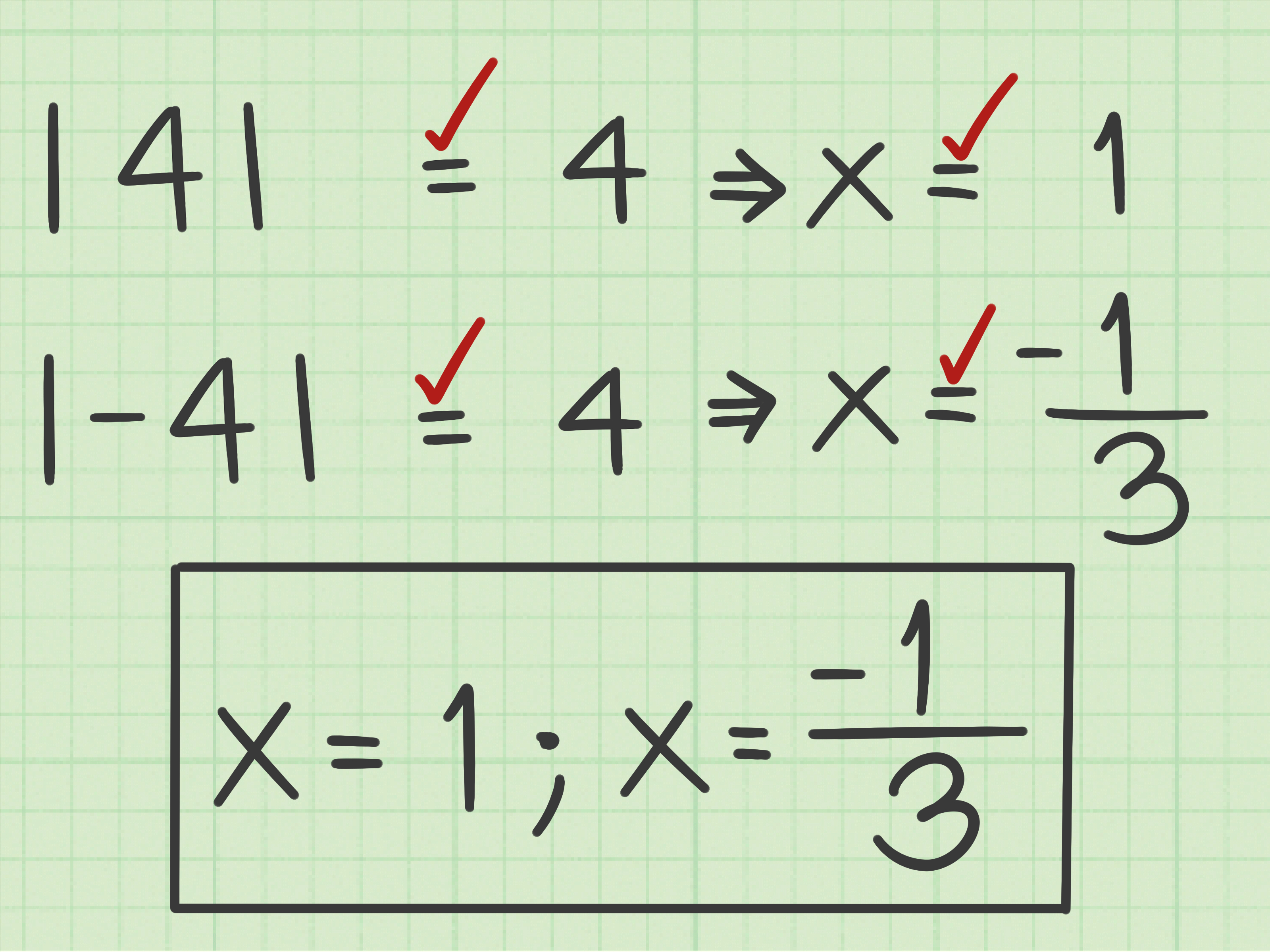
Understanding the Enigma of Absolute Value Equations

Absolute value equations, though seemingly simple, can present a unique challenge, especially when solving them. The concept of absolute value itself is straightforward—it represents the distance of a number from zero on the number line, regardless of direction. However, when it comes to equations, this simplicity can transform into a complex puzzle.

Solving absolute value equations requires a systematic approach and a solid understanding of mathematical principles. These equations often involve unknown variables hidden within the absolute value bars, making it a game of unraveling the mystery to find the correct solution.

Let’s embark on this mathematical journey, breaking down the steps to solve absolute value equations and mastering the art of unlocking their secrets.

The Fundamental Steps to Solve Absolute Value Equations

Solving absolute value equations involves a series of logical steps, each building upon the other. Here’s a systematic approach to tackle these equations:

1. Identify the Absolute Value Expression: Start by identifying the absolute value expression in the equation. This is usually represented by vertical bars enclosing a variable, such as |x|.

2. Consider the Two Possible Cases: Absolute value equations often have two cases to consider. This is because the variable inside the absolute value bars can be either positive or negative, and both possibilities need to be explored.

3. Set Up Two Equations: Create two separate equations, one for each case. For instance, if the original equation is |x| = 5, you would create two equations: x = 5 and -x = 5.

4. Solve Each Equation: Solve the two equations independently. In the above example, you would find that x = 5 and -x = -5, which gives you x = 5 as the solution.

5. Check Your Solution: Always verify your solution by plugging it back into the original equation. This step is crucial to ensure the accuracy of your answer.

Dealing with More Complex Absolute Value Equations

While the above steps provide a basic framework, absolute value equations can get more intricate. When dealing with equations involving multiple terms or more complex expressions, the process becomes slightly nuanced.

Mastering the Art: Advanced Techniques

For more advanced absolute value equations, the process can be a bit more involved. These equations often require a deeper understanding of mathematical concepts and creative problem-solving skills.

Here are some advanced techniques to tackle these complex equations:

• Simplify the Equation: Sometimes, simplifying the equation can make it more manageable. This could involve combining like terms, factoring, or using other algebraic manipulations.

• Use Properties of Absolute Value: Understanding the properties of absolute value can be crucial. For instance, the triangle inequality |x + y| ≤ |x| + |y| can be a powerful tool in certain scenarios.

• Graphical Approach: In some cases, visualizing the equation on a number line or graph can provide insights and help narrow down the solution.

• Try Different Cases: If the equation doesn't seem to yield a solution, consider trying different cases or rearranging the terms to gain a new perspective.

Practice Makes Perfect: Sample Problems

To truly master the art of solving absolute value equations, practice is key. Here are some sample problems to sharpen your skills:

Conclusion: The Beauty of Mathematical Precision

Solving absolute value equations is an art that requires precision, logical thinking, and a deep understanding of mathematical principles. While these equations can present a challenge, with practice and the right techniques, they can be mastered.

Remember, mathematics is a journey of exploration and discovery. Embrace the enigma of absolute value equations, and let your mathematical skills guide you to the solution.