Mastering Absolute Value: 5 Key Tips

The concept of absolute value is a fundamental mathematical tool with wide-ranging applications, from basic arithmetic to advanced calculus and beyond. It’s essential for any mathematician or student of mathematics to grasp this concept thoroughly. Absolute value represents the distance of a number from zero on a number line, regardless of direction. In other words, it tells us how far a number is from the origin, stripping away any negative signs. Here, we’ll explore five essential tips to help you master absolute value, making it an intuitive and powerful tool in your mathematical arsenal.
Understanding absolute value is crucial for many areas of mathematics, and these tips will help solidify your grasp of this fundamental concept.
1. Visualize the Number Line

The number line is an invaluable tool for understanding absolute value. Imagine a straight line with zero at its center and negative and positive numbers stretching out in both directions. When you think of absolute value, picture the distance between any number and the zero point. For example, consider the number -5. Its absolute value is 5, because it’s five units away from zero, whether you’re counting left or right.
Visualizing absolute value on a number line helps you develop an intuitive sense of distance and magnitude. It's a powerful way to reinforce your understanding and make calculations easier.
2. Memorize Common Absolute Values
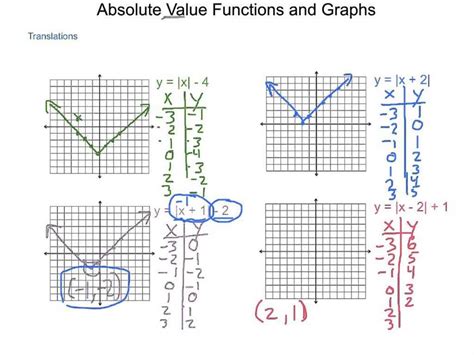
While you don’t need to memorize every absolute value, familiarizing yourself with some common ones can greatly simplify your calculations. For instance, the absolute value of 0 is 0, because it’s zero units away from the origin. Similarly, the absolute value of 3 is 3, and the absolute value of -3 is also 3, as they’re both three units away from zero.
- Absolute value of 0 = 0
- Absolute value of 3 = 3
- Absolute value of -3 = 3
3. Use Absolute Value in Equations and Inequalities
Absolute value is a versatile tool that’s often used in equations and inequalities to solve for unknown variables. When you encounter an absolute value equation or inequality, remember that the absolute value function returns the distance from zero, which can be positive or negative. For example, consider the equation |x| = 4. This means that the distance of x from zero is 4 units, so x could be either 4 or -4.
Pros: Using absolute value in equations and inequalities can provide multiple solutions or restrict solutions to a specific range.
Cons: Solving absolute value equations can be a bit trickier, as you often need to consider multiple cases.
4. Apply Absolute Value in Real-World Scenarios
Absolute value has numerous real-world applications, especially in fields like physics, engineering, and economics. For instance, it can represent temperature variations, speed differences, or profit margins. When applying absolute value in these contexts, remember that it represents the magnitude of a change, ignoring the direction.
In the real world, absolute value helps quantify the magnitude of changes, whether it's the rise and fall of stock prices or the fluctuation of temperatures.
5. Practice, Practice, Practice!

Like any mathematical concept, mastering absolute value takes practice. Solve a variety of problems involving absolute value to reinforce your understanding. Practice not only helps you become more comfortable with the concept but also improves your problem-solving skills.
How do I know when to use absolute value in an equation or inequality?
+Absolute value is often used when the distance or magnitude is important, rather than the direction. If you're dealing with a problem where you need to find the distance from a certain point or the magnitude of a change, absolute value is likely involved.
Can absolute value ever be negative?
+No, absolute value is always positive or zero. The whole point of absolute value is to strip away any negative signs, so it represents only the magnitude, not the direction.
How is absolute value different from regular numbers or variables?
+Regular numbers and variables represent specific values or unknowns, while absolute value represents the distance from zero. It's a tool to measure magnitude, not direction.
Are there any shortcuts for calculating absolute value?
+Not really, as calculating absolute value is quite straightforward. Just remember that it's the distance from zero, so you don't need to consider direction.
Remember, absolute value is a powerful mathematical tool, and these tips will help you harness its potential. With practice and a strong understanding of the concept, you’ll be able to tackle absolute value problems with ease.