The Ultimate Guide to Graphing Exponential Functions

Exponential functions are a powerful mathematical tool with applications spanning various fields, from finance to biology and physics. Understanding how to graph these functions is a crucial skill for any student or professional working with data and mathematical models. This guide will delve into the intricacies of graphing exponential functions, providing you with the knowledge and techniques to master this essential skill.

Understanding Exponential Functions

Exponential functions are mathematical expressions that involve an exponent, often represented as a base raised to a variable power. The general form of an exponential function is given by:

\[ f(x) = a \cdot b^x\]

Where: - f(x) represents the function. - a is a constant that determines the vertical shift (or initial value) of the graph. - b is the base of the exponent, which can be any positive real number, but is often 2, e (the mathematical constant approximately equal to 2.71828), or 10. - x is the independent variable, which can be any real number.

The key characteristic of exponential functions is that they exhibit rapid growth or decay as the input value x increases or decreases. This property makes them particularly useful for modeling phenomena that involve exponential growth or decay, such as population growth, compound interest, and radioactive decay.

Graphing Exponential Functions: A Step-by-Step Guide

Step 1: Choose an Appropriate Base

The choice of the base b in an exponential function significantly influences the shape and behavior of the graph. Here’s a breakdown of the most commonly used bases and their characteristics:

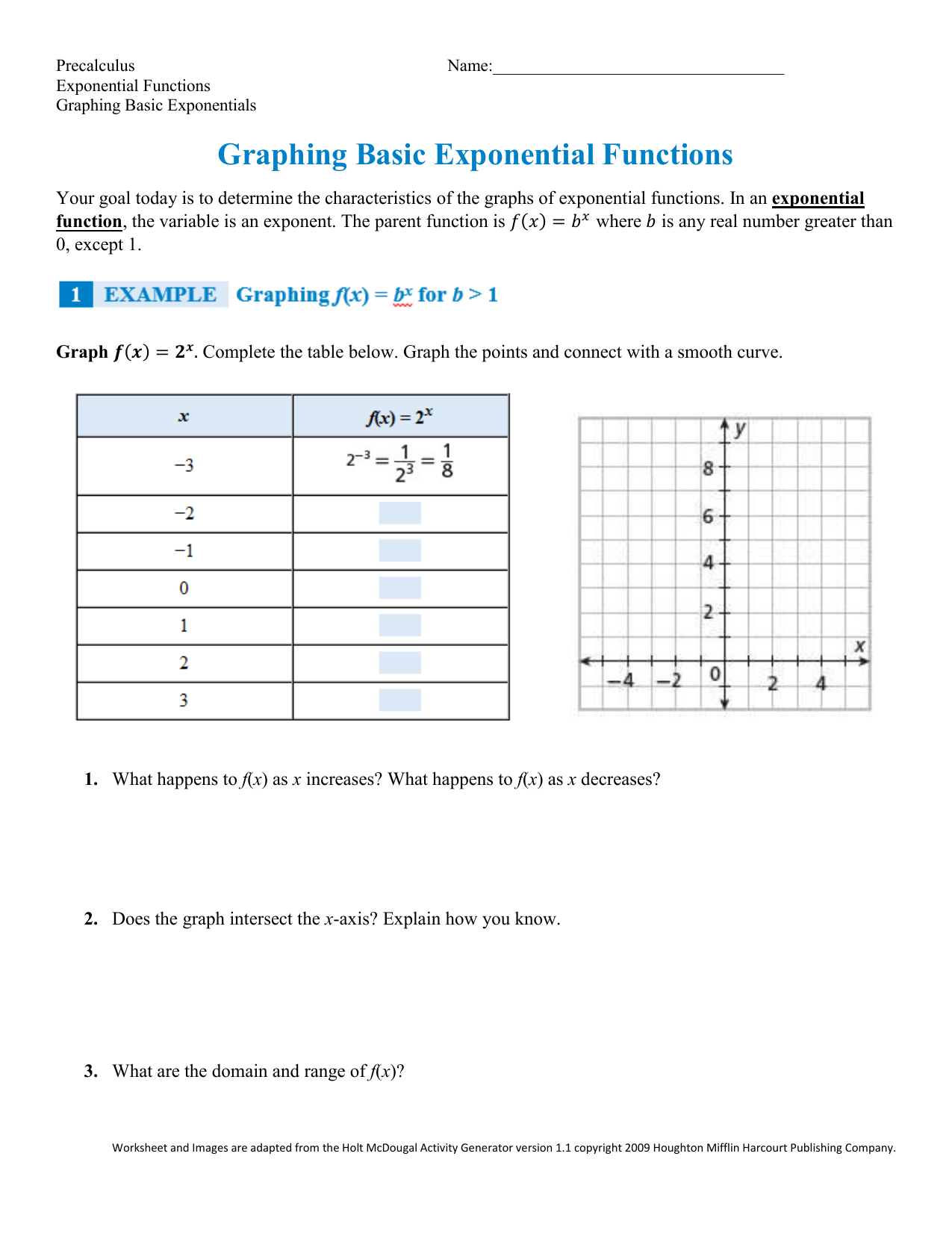
• Base b = 2: Exponential Growth and Decay

  • Exponential functions with a base of 2 often represent binary or digital systems, such as computer science applications.
  • The graph of f(x) = 2^x exhibits rapid growth for positive x values and rapid decay for negative x values.
  • This function has a vertical asymptote at x = 0, where the graph approaches infinity as x approaches zero from the right and negative infinity as x approaches zero from the left.

• Base b = e: The Natural Exponential Function

  • The natural exponential function, f(x) = e^x, is perhaps the most important and widely used exponential function in mathematics and science.
  • The number e (approximately equal to 2.71828) is a mathematical constant that arises naturally in many areas, including calculus, probability, and physics.
  • The graph of f(x) = e^x is always positive and increases steadily without bounds as x increases. It has a unique property: the slope of the tangent line at any point on the graph is equal to the y-coordinate of that point.

• Base b = 10: Scientific and Decimal Applications

  • Exponential functions with a base of 10 are commonly used in scientific and decimal applications, such as measuring magnitudes (e.g., the Richter scale for earthquakes).
  • The graph of f(x) = 10^x exhibits rapid growth for positive x values and rapid decay for negative x values, similar to the b = 2 case.
  • The graph has a vertical asymptote at x = 0, and the y-intercept is always 1, regardless of the value of the constant a.

Step 2: Determine the Domain and Range

The domain of an exponential function is the set of all real numbers for which the function is defined. For all three bases discussed above, the domain is (-\infty, \infty).

The range of an exponential function, on the other hand, depends on the value of the base b.

• For b > 1, the range is (0, \infty).
• For b = 1, the range is \{1\}.
• For 0 < b < 1, the range is (\infty, 0).

Step 3: Identify Key Features of the Graph

When graphing exponential functions, it’s essential to identify the key features that help characterize the shape and behavior of the graph. These include:

• Vertical Asymptote: Exponential functions often have a vertical asymptote at x = k, where k is a critical value that causes the function to become undefined. For the functions discussed above, the vertical asymptote is at x = 0.

• y-Intercept: The y-intercept of an exponential function is the point where the graph intersects the y-axis, and it’s given by f(0) = a. This point represents the initial value or the starting point of the function.

• Growth or Decay Rate: The growth or decay rate of an exponential function is determined by the base b. As discussed earlier, a base greater than 1 results in exponential growth, while a base between 0 and 1 results in exponential decay.

Step 4: Sketch the Graph

With the key features identified, you can now sketch the graph of the exponential function. Here’s a general strategy:

• Start by plotting the y-intercept (0, a).
• Determine the behavior of the function as x approaches negative infinity and positive infinity. This will help you sketch the general shape of the graph.
• If there is a vertical asymptote, sketch it lightly as a guide.
• Use the growth or decay rate to decide whether the graph should curve upwards (growth) or downwards (decay) as x increases.
• Finally, connect the dots and smooth out the curve to create the exponential graph.

Advanced Techniques for Graphing Exponential Functions

Transformation of Exponential Functions

Exponential functions can be transformed in various ways to model different scenarios. The most common transformations include:

• Vertical Shift: Adding or subtracting a constant inside the function, f(x) = a \cdot b^{x + c}, results in a vertical shift of the graph. The graph is shifted up by c units if c is positive and down by c units if c is negative.

• Horizontal Shift: Multiplying the input x by a constant, f(x) = a \cdot b^{kx}, results in a horizontal shift of the graph. The graph is shifted to the right by \frac{1}{k} units if k is positive and to the left by \frac{1}{k} units if k is negative.

• Reflection: Multiplying the function by -1, f(x) = -a \cdot b^x, results in a reflection across the x-axis. This changes the direction of the curve, from growth to decay or vice versa.

Exponential Functions with Complex Bases

While the bases b = 2, e, and 10 are commonly used, exponential functions can have any positive real number as their base. For example, consider the function f(x) = 3^x. This function exhibits similar characteristics to the b = 2 case, but with a different growth or decay rate.

Applications of Exponential Functions

Exponential functions find applications in a wide range of fields:

• Finance: Exponential functions are used to model compound interest, population growth, and inflation rates.

• Biology: Population growth, radioactive decay, and bacterial growth are often modeled using exponential functions.

• Physics: The decay of radioactive materials and the growth of certain physical processes, such as the spread of sound waves, can be described by exponential functions.

• Computer Science: Binary exponential functions (b = 2) are fundamental in digital systems and algorithms.

• Engineering: Exponential functions are used in signal processing, control systems, and modeling of various physical processes.

Conclusion

Graphing exponential functions is a powerful skill that allows us to visualize and understand complex mathematical models. By understanding the key features, domains, ranges, and transformations of exponential functions, we can effectively represent and analyze a wide range of real-world phenomena. Whether you’re a student studying mathematics or a professional working with data, mastering the art of graphing exponential functions is a valuable asset.

Frequently Asked Questions (FAQ)