Graphing Equations: A Visual Guide
Welcome to the world of graphing equations, a powerful tool that brings mathematical concepts to life! In this visual guide, we will embark on a journey to explore the art and science of graphing, uncovering the secrets behind transforming equations into captivating visual representations. Whether you are a student delving into the fundamentals of mathematics or a professional seeking a deeper understanding of data visualization, this comprehensive guide will equip you with the knowledge and skills to master the art of graphing.
The Fundamentals of Graphing Equations

Graphing equations is a fundamental skill in mathematics, offering a unique perspective on mathematical relationships. It allows us to visualize abstract concepts, making them more tangible and easier to comprehend. By plotting points and connecting them, we can unveil the beauty of mathematical curves and uncover the hidden patterns within equations.
At its core, graphing equations involves mapping mathematical expressions onto a coordinate plane, also known as a Cartesian plane. This plane consists of two perpendicular lines, the x-axis (horizontal) and the y-axis (vertical), intersecting at a point called the origin. Each point on this plane is identified by its coordinates, denoted as (x, y), where x represents the distance along the x-axis and y represents the distance along the y-axis.
Linear Equations: The Basics
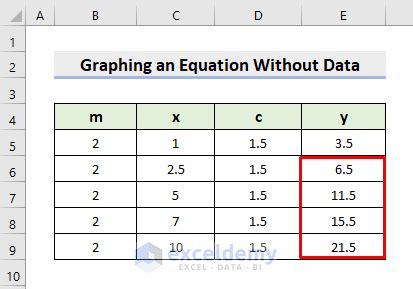
Let’s begin our exploration with linear equations, one of the simplest and most fundamental types of equations. Linear equations describe straight lines on a coordinate plane. They take the form of y = mx + b, where m represents the slope of the line and b represents the y-intercept, which is the point where the line intersects the y-axis.
To graph a linear equation, we follow a straightforward process. First, we identify the slope, m, and the y-intercept, b. The slope determines the steepness and direction of the line. A positive slope indicates an upward direction, while a negative slope indicates a downward direction. The y-intercept is the starting point of the line, where it crosses the y-axis.
Once we have identified these values, we can plot the y-intercept on the coordinate plane. From there, we use the slope to determine the direction and magnitude of the line. For example, if the slope is 2, we move 2 units up and 1 unit to the right to find the next point. We repeat this process, connecting the points to form a straight line.
Consider the equation y = 3x + 2. In this equation, the slope is 3, indicating an upward direction, and the y-intercept is 2. By plotting the y-intercept (0, 2) and using the slope to find additional points, we can create a straight line on the coordinate plane.
Quadratic Equations: Unveiling Curves
While linear equations produce straight lines, quadratic equations introduce a whole new dimension to graphing. Quadratic equations describe parabolas, which are U-shaped curves. They take the form of y = ax^2 + bx + c, where a, b, and c are coefficients that determine the shape and position of the parabola.
Graphing quadratic equations involves finding the vertex, which is the highest or lowest point of the parabola, and the axis of symmetry, which is a vertical line that divides the parabola into two symmetrical halves. The vertex is given by the coordinates (h, k), where h is the x-coordinate and k is the y-coordinate.
To find the vertex, we can use the formula h = -b / (2a). Once we have the x-coordinate, we can substitute it back into the equation to find the corresponding y-coordinate, k. The axis of symmetry is then given by the line x = h.
For example, let's consider the equation y = 2x^2 - 4x + 3. By applying the formula, we find that h = -b / (2a) = -(-4) / (2 * 2) = 1. Substituting x = 1 into the equation, we find the corresponding y-coordinate, k = 2(1)^2 - 4(1) + 3 = 5. Thus, the vertex of the parabola is (1, 5), and the axis of symmetry is x = 1.
Advanced Graphing Techniques

As we delve deeper into the world of graphing equations, we encounter more complex equations and advanced techniques. These techniques allow us to explore a wide range of mathematical concepts and uncover the beauty of higher-order equations.
Exponential and Logarithmic Functions
Exponential and logarithmic functions are powerful mathematical tools that find applications in various fields, including finance, physics, and biology. Graphing these functions reveals their unique characteristics and behavior.
Exponential functions, such as y = 2^x, exhibit rapid growth or decay as x increases or decreases. The graph of an exponential function forms a curve that rises or falls sharply, depending on the base of the exponent. On the other hand, logarithmic functions, such as y = log(x), describe the inverse relationship between two variables. The graph of a logarithmic function forms an upward-sloping curve that approaches the x-axis asymptotically.
To graph exponential and logarithmic functions, we can use a combination of analytical methods and technology. By evaluating the function at specific points and connecting the points, we can create a visual representation of the function's behavior. Additionally, graphing calculators and software provide powerful tools for plotting these functions accurately and efficiently.
Trigonometric Functions: Exploring Periodic Behavior
Trigonometric functions, such as sine, cosine, and tangent, describe periodic behavior and find applications in various fields, including physics, engineering, and signal processing. Graphing trigonometric functions reveals their oscillatory nature and unique patterns.
For example, the sine function, y = sin(x), produces a wave-like curve that repeats itself at regular intervals. The graph of the sine function forms a sinusoidal curve, with a period of 2π, meaning that the curve repeats every 2π units along the x-axis. The cosine function, y = cos(x), is similar to the sine function but has a phase shift, resulting in a different pattern.
To graph trigonometric functions, we can use a combination of mathematical principles and technology. By understanding the properties of these functions, such as their amplitudes, periods, and phase shifts, we can accurately plot their graphs. Graphing calculators and software provide valuable tools for visualizing trigonometric functions, allowing us to explore their behavior and make predictions.
Applications of Graphing Equations
Graphing equations is not limited to theoretical mathematics; it has numerous practical applications across various fields. From physics and engineering to economics and social sciences, graphing equations provides a powerful tool for analyzing and understanding real-world phenomena.
Physics and Engineering
In physics and engineering, graphing equations is essential for modeling and analyzing physical systems. For example, graphing the position-time graph of an object in motion allows us to visualize its velocity and acceleration. By plotting the position of the object at different times, we can create a curve that represents its motion, helping us understand its behavior and make predictions.
Additionally, graphing equations is crucial in electrical engineering for analyzing circuits. By plotting voltage and current values against time, engineers can visualize the behavior of electrical systems, identify potential issues, and optimize circuit designs.
Economics and Social Sciences
Graphing equations finds applications in economics and social sciences for modeling and analyzing economic trends and social phenomena. For instance, graphing supply and demand curves helps economists understand market dynamics and make predictions about price fluctuations. By plotting the supply and demand functions on a coordinate plane, economists can visualize the equilibrium point where the curves intersect, representing the market price and quantity.
Similarly, in social sciences, graphing equations is used to model and analyze social networks. By representing individuals as nodes and relationships as edges, researchers can visualize the structure and dynamics of social networks, gaining insights into social behavior and patterns.
Conclusion: The Power of Visualization
Graphing equations is a powerful tool that transforms abstract mathematical concepts into tangible visual representations. It allows us to explore the beauty and complexity of mathematical relationships, unlocking new insights and understanding. From linear equations to exponential and trigonometric functions, graphing provides a window into the fascinating world of mathematics.
By mastering the art of graphing, we gain a deeper appreciation for the elegance and practicality of mathematics. It empowers us to analyze real-world phenomena, make predictions, and solve complex problems. Whether in physics, engineering, economics, or social sciences, graphing equations serves as a valuable tool for unlocking the secrets of the universe and driving innovation.
As we conclude our journey through the world of graphing equations, we hope that this visual guide has inspired and equipped you with the knowledge and skills to continue exploring the wonders of mathematics. Remember, graphing is not just a technical skill but an art form, where equations come to life and reveal their hidden stories.
How do I choose the appropriate scale for my graph?
+Choosing the appropriate scale for your graph depends on the range of values your data covers. It’s important to select a scale that accurately represents your data without overcrowding or underrepresenting any values. Start by examining the minimum and maximum values in your dataset and consider the level of detail you want to showcase. For instance, if your data covers a wide range, you might opt for a larger scale to prevent overcrowding. Conversely, if your data is more concentrated, a smaller scale may be suitable to highlight finer details.
What are some common mistakes to avoid when graphing equations?
+When graphing equations, it’s crucial to avoid common mistakes that can lead to inaccurate representations. Firstly, ensure that you correctly identify the type of equation you are dealing with, as this determines the appropriate graphing technique. Secondly, pay close attention to the scale and axis labels to ensure they accurately represent the data. Misaligned scales or incorrect labels can lead to misinterpretations. Lastly, double-check your calculations and ensure that you have plotted the correct points on the graph.
Can graphing equations be used to make predictions?
+Absolutely! Graphing equations is a powerful tool for making predictions and analyzing trends. By examining the behavior of the graph and identifying patterns, you can make informed predictions about future values or outcomes. For example, in physics, graphing the motion of an object allows you to predict its position or velocity at a given time. Similarly, in economics, graphing supply and demand curves helps predict market prices.



