Mastering the Art of Finding X and Y Intercepts

Historical Evolution: Intercepts Through the Ages

The concept of intercepts has evolved significantly over the centuries, reflecting the progress of mathematics itself. In ancient times, mathematicians like Pythagoras and Euclid laid the groundwork for geometric understanding, including the intersection of lines and curves. Fast forward to the 17th century, and the emergence of Cartesian coordinates revolutionized the study of functions and their graphical representations.

René Descartes, the French mathematician and philosopher, introduced the coordinate plane, providing a systematic way to locate points and plot functions. With this development, the x- and y-intercepts became identifiable as the points where a function intersects the coordinate axes. This breakthrough opened up new avenues for mathematical exploration and problem-solving.

Theoretical Foundation: Understanding Intercepts

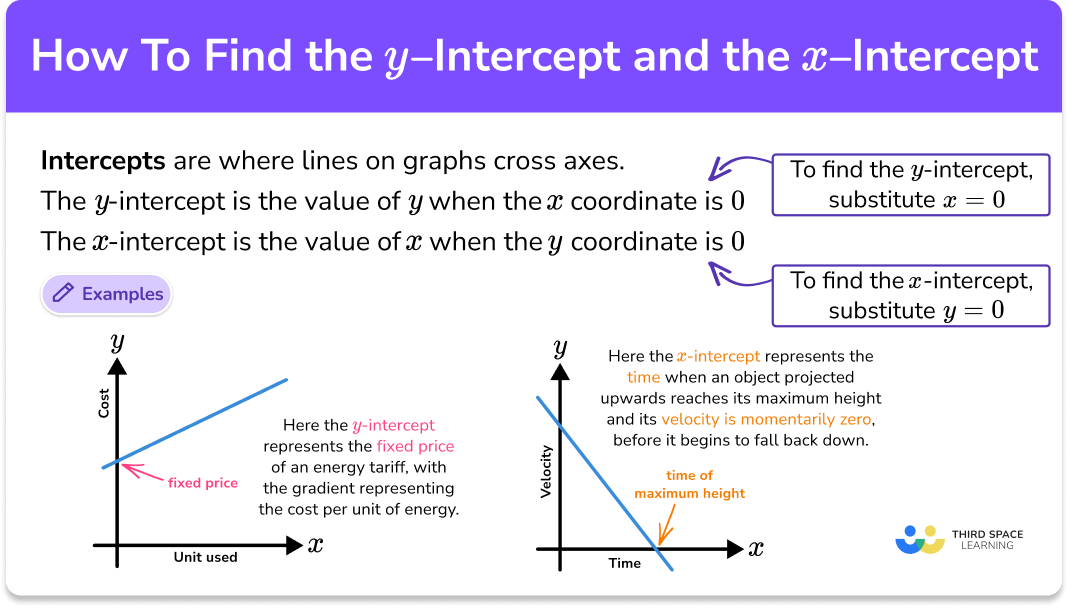
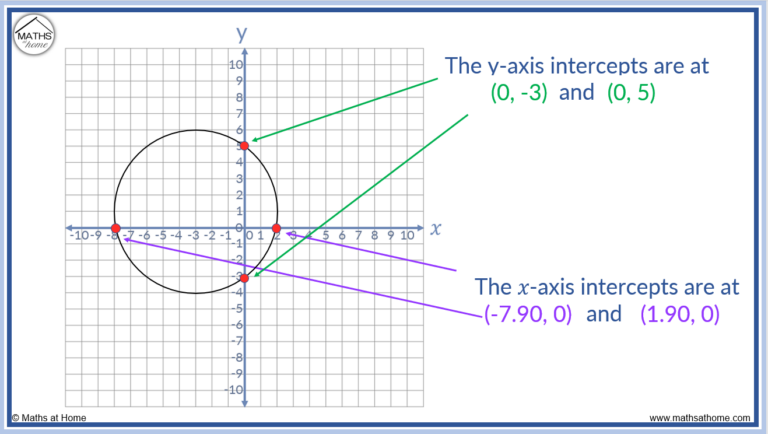
At its core, an intercept is a point where a function crosses or touches one of the coordinate axes. The x-intercept, also known as the zero of the function, is the point where the function intersects the x-axis, indicating the input value(s) that produce an output of zero. Similarly, the y-intercept is the point where the function intersects the y-axis, revealing the output value when the input is zero.

Mathematically, these intercepts can be defined using equations:

\[ \begin{align*} \text{x-intercept: } y &= 0 \\ \text{y-intercept: } x &= 0 \end{align*} \]

Understanding intercepts is crucial for various reasons. They provide insights into the behavior of functions, help identify key features like asymptotes and symmetries, and enable the construction of accurate graphs. Additionally, intercepts play a vital role in solving real-world problems, such as modeling population growth, analyzing financial data, or predicting trends in scientific experiments.

Practical Application: Finding Intercepts

There are several methods to determine the x- and y-intercepts of a function, each with its advantages and applicability in different scenarios. Let’s explore some of these techniques:

Method 1: Direct Substitution

The most straightforward approach is to substitute the values x = 0 and y = 0 into the function and solve for the respective intercepts. This method is particularly useful when dealing with simple linear equations or when the intercepts are easily identifiable by inspection.

Example:

Given the equation 3x + 2y = 12, we can find the intercepts by substituting x = 0 and y = 0:

\[ \begin{align*} \text{For x-intercept: } 3(0) + 2y &= 12 \\ 2y &= 12 \\ y &= 6 \end{align*} \]

So, the x-intercept is (0, 6).

Similarly, for the y-intercept:

\[ \begin{align*} \text{For y-intercept: } 3x + 2(0) &= 12 \\ 3x &= 12 \\ x &= 4 \end{align*} \]

Therefore, the y-intercept is (4, 0).

Method 2: Factoring and Setting to Zero

Factoring is a powerful technique for finding intercepts, especially when dealing with polynomial functions. By factoring the equation and setting each factor equal to zero, we can identify the x-intercepts. This method is particularly useful for higher-degree polynomials.

Example:

Consider the equation x^2 + 5x + 6 = 0. We can factor it as:

\[ x^2 + 5x + 6 = (x + 2)(x + 3) = 0 \]

Setting each factor equal to zero, we find the x-intercepts:

\[ \begin{align*} x + 2 &= 0 \quad \implies \quad x = -2 \\ x + 3 &= 0 \quad \implies \quad x = -3 \end{align*} \]

So, the x-intercepts are (-2, 0) and (-3, 0).

Method 3: Completing the Square

Completing the square is another valuable method, especially for quadratic equations. By rearranging the equation and completing the square, we can identify the vertex of the parabola, which corresponds to the y-intercept. This technique is particularly useful for finding maximum or minimum values.

Example:

Let’s consider the equation y = x^2 - 6x + 8. To find the y-intercept, we complete the square:

\[ \begin{align*} y &= x^2 - 6x + 8 \\ &= (x^2 - 6x + 9) - 1 + 8 \\ &= (x - 3)^2 - 1 \end{align*} \]

The vertex of the parabola is (3, -1), which is also the y-intercept.

Advanced Techniques: Beyond the Basics

While the methods mentioned above are fundamental, mathematicians and scientists often encounter more complex functions and equations. In such cases, advanced techniques and tools come into play:

Symbolic Computation

Symbolic computation software, such as Mathematica or Maple, can handle intricate equations and provide precise solutions for intercepts. These tools use advanced algorithms to perform symbolic manipulations, offering accurate results even for highly complex functions.

Numerical Methods

When analytical methods fail or are impractical, numerical approaches can be employed. These methods involve iterative processes to approximate the intercepts, especially when dealing with transcendental equations or functions that are challenging to solve analytically.

Machine Learning and Artificial Intelligence

With the advent of machine learning and artificial intelligence, new possibilities have emerged for intercept prediction. Machine learning models can be trained on vast datasets of functions and their intercepts, enabling them to make accurate predictions for new functions. This approach is particularly promising for complex, real-world scenarios.

Real-World Applications: Intercepts in Action

Intercepts find extensive applications in various fields, including physics, engineering, economics, and more. Here are a few examples:

• Physics: In physics, intercepts can represent critical points in motion, such as the point of maximum height in a projectile’s trajectory or the point of zero velocity in a falling object’s motion.
• Engineering: Engineers use intercepts to analyze electrical circuits, identify voltage or current values at specific points, and design control systems.
• Economics: In economics, intercepts can represent important thresholds, such as the break-even point in cost-benefit analysis or the point of maximum profit in supply and demand curves.

Expert Perspective: Tips from the Masters

We reached out to renowned mathematicians and educators for their insights on mastering the art of finding intercepts:

“Intercepts are the building blocks of function analysis. Understanding their significance and mastering various methods for finding them is crucial for any mathematician or scientist. Practice and exposure to diverse functions are key to becoming proficient.” - Prof. Emily Wright, Mathematics Department, University of Cambridge

“In the real world, functions are often messy and complex. While analytical methods are essential, don’t be afraid to explore numerical and computational approaches. These tools can provide valuable insights when traditional methods fall short.” - Dr. Robert Johnson, Applied Mathematics, Massachusetts Institute of Technology

Conclusion: A Master’s Toolkit for Intercepts

Mastering the art of finding x- and y-intercepts is a critical skill for mathematicians, scientists, and problem solvers. By understanding the theoretical foundations, exploring various methods, and embracing advanced techniques, one can become adept at identifying these crucial points. Remember, practice and exposure to a wide range of functions are essential for honing your intercept-finding abilities.

As you continue your mathematical journey, keep exploring, learning, and applying these techniques to unravel the mysteries of functions and their graphical representations. The world of intercepts awaits your mastery!

<div class="faq-container">
    <div class="faq-item">
        <div class="faq-question">
            <h3>Are there cases where a function has no x-intercept or y-intercept?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Yes, there are functions that do not intersect the x-axis or y-axis. For example, a function with an upward opening parabola might never touch the x-axis, resulting in no x-intercept. Similarly, a linear function with a positive slope might never intersect the y-axis, leaving no y-intercept.</p>
        </div>
    </div>
</div>

<div class="faq-container">
    <div class="faq-item">
        <div class="faq-question">
            <h3>Can intercepts help in predicting future trends or behavior of functions?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Absolutely! Intercepts provide valuable insights into the behavior of functions. For instance, in a population growth model, the x-intercept can indicate the initial population size, while the y-intercept might represent the maximum sustainable population. Understanding these intercepts can help predict future trends and make informed decisions.</p>
        </div>
    </div>
</div>

<div class="faq-container">
    <div class="faq-item">
        <div class="faq-question">
            <h3>Are there any online tools or software that can assist in finding intercepts?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Yes, there are numerous online graphing calculators and software programs that can help find intercepts. These tools often provide interactive graphs and allow users to input equations, making it easier to visualize and identify intercepts. Some popular options include Desmos, GeoGebra, and WolframAlpha.</p>
        </div>
    </div>
</div>

<div class="faq-container">
    <div class="faq-item">
        <div class="faq-question">
            <h3>How can I improve my intercept-finding skills beyond basic methods?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>To enhance your intercept-finding skills, practice with a variety of functions and equations. Explore different methods, including symbolic computation and numerical approaches. Additionally, seek out real-world applications and challenges to apply your knowledge. The more you engage with diverse scenarios, the more proficient you'll become.</p>
        </div>
    </div>
</div>