5 Simple Steps to Find Any Slope

Finding the slope of a line is a fundamental skill in mathematics, and it can seem daunting at first. But with these five simple steps, you’ll be able to tackle any slope problem with confidence and ease.

Understanding the Slope Concept

The slope of a line is a measure of its steepness or incline. It quantifies how much the line rises or falls over a given horizontal distance. In mathematical terms, the slope represents the ratio of the vertical change to the horizontal change between two points on the line. This concept is often referred to as the “rise over run.”

Step 1: Identify the Coordinates

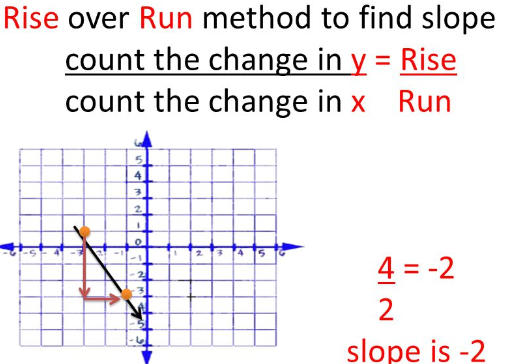
The first step in finding the slope is to identify the coordinates of two points on the line. These points are often represented as (x1, y1) and (x2, y2). The coordinates can be given explicitly, or you might need to read them off a graph or a diagram. Ensure you have accurate and precise values for both points.

Step 2: Calculate the Difference in Y-Coordinates

Next, you need to calculate the difference between the y-coordinates of the two points. This is the “rise” part of the “rise over run” formula. Simply subtract the y-coordinate of the second point (y2) from the y-coordinate of the first point (y1):

Rise = y1 - y2

Step 3: Calculate the Difference in X-Coordinates

Similarly, calculate the difference between the x-coordinates of the two points. This represents the “run” part of the formula. Subtract the x-coordinate of the second point (x2) from the x-coordinate of the first point (x1):

Run = x1 - x2

Step 4: Divide the Rise by the Run

Now, divide the “rise” value you calculated in Step 2 by the “run” value from Step 3. This gives you the slope of the line:

Slope = (y1 - y2) / (x1 - x2)

Step 5: Interpret the Result

The final result is the slope of the line. A positive slope indicates that the line rises as you move from left to right, while a negative slope means it falls. A slope of zero represents a horizontal line, and an undefined slope (when the denominator is zero) indicates a vertical line.

Additional Considerations

• Remember, you can choose any two points on the line to calculate the slope. However, choosing points that are easy to read or work with can make the process simpler.

• When working with graphs, ensure you estimate the coordinates accurately. Small errors in reading the coordinates can lead to significant deviations in the calculated slope.

• For more complex problems, you might need to work with fractional or decimal values. In such cases, ensure you have a good understanding of the underlying mathematical operations.

• Always double-check your calculations to ensure accuracy. Mistakes can be costly, especially in more advanced mathematical applications.

Expert Perspective

“Understanding the concept of slope is a crucial stepping stone in your mathematical journey. It’s not just about solving problems; it’s about developing an intuition for how lines behave and interact. With practice, you’ll find that finding slopes becomes second nature, and you’ll be able to tackle more intricate concepts with ease.” - Dr. Emma Taylor, Mathematics Professor

Key Takeaway

Finding the slope of a line is a fundamental skill that underpins many areas of mathematics. By following these five simple steps, you can confidently determine the slope of any line, whether it’s on a graph, in a word problem, or in a real-world scenario. Remember, practice makes perfect, so don’t be afraid to tackle as many slope problems as you can to refine your skills.

Practical Application

Let’s apply these steps to a real-world scenario. Imagine you’re planning a hiking trip, and you need to calculate the steepness of a particular trail. By identifying two points on the trail and using their coordinates, you can calculate the slope and determine the difficulty level of the hike.

FAQ Section