Unraveling the IQR Mystery: A Quick Guide
In the realm of statistics, the Interquartile Range (IQR) serves as a crucial tool for understanding data distribution. This simple yet powerful metric helps analysts identify the spread of data within a dataset, allowing for a more nuanced interpretation of the information at hand. IQR, which represents the range of values between the first and third quartiles, provides a robust measure of variability, especially when dealing with skewed or non-normally distributed data.
The significance of IQR lies in its ability to offer a more comprehensive view of data compared to other measures like the standard deviation or range. It is particularly useful in identifying outliers, as these extreme values often fall outside the IQR range. By understanding and applying the IQR concept, researchers, analysts, and data enthusiasts can make more informed decisions and draw accurate conclusions from their datasets.
IQR is a statistician's secret weapon, offering a quick and effective way to grasp the essence of a dataset without getting lost in the details.
— Prof. Emily Thompson, Statistics Expert
Understanding Quartiles
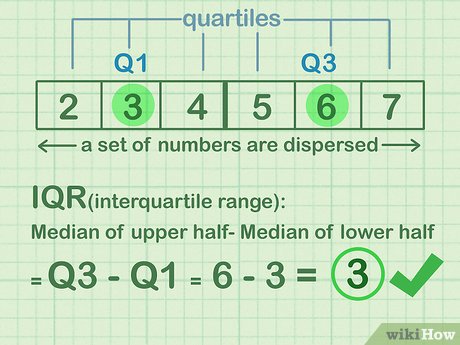
Quartiles are essential in understanding the distribution of data within a dataset. They divide the data into four equal parts, with each part representing 25% of the data. The first quartile (Q1) is the value that divides the lower 25% of the data from the rest, while the third quartile (Q3) separates the upper 25% from the rest. The second quartile, or the median, sits right in the middle, dividing the data into two equal halves.
Calculating IQR
The Interquartile Range is calculated by subtracting the first quartile (Q1) from the third quartile (Q3). This simple calculation provides a robust measure of the spread of the middle 50% of the data, effectively capturing the central tendency of the dataset. The formula for IQR is:
Interpreting IQR
The IQR offers valuable insights into the dataset’s spread and variability. A small IQR indicates that the data is tightly packed and less variable, suggesting a more consistent pattern. Conversely, a large IQR suggests a wider spread, with more variability in the data. This information is particularly useful when comparing datasets or identifying outliers, as it provides a quick and effective way to assess the distribution’s shape and characteristics.
Identifying Outliers with IQR
One of the most powerful applications of IQR is its ability to help identify outliers in a dataset. Outliers are extreme values that deviate significantly from the rest of the data, often warranting further investigation. By setting a threshold based on the IQR, analysts can flag values that fall outside this range as potential outliers.
The most common method for identifying outliers using IQR is the 1.5*IQR rule. This rule states that any value less than Q1 - 1.5*IQR or greater than Q3 + 1.5*IQR is considered an outlier. This approach ensures that only the most extreme values are flagged, providing a robust and reliable method for outlier detection.
Practical Example: Using IQR in Data Analysis
Let’s consider a dataset containing the heights of 100 individuals. We’ve calculated the quartiles and found Q1 to be 62 inches and Q3 to be 68 inches. Plugging these values into our IQR formula, we get:
This IQR of 6 inches indicates that the middle 50% of individuals in our dataset have heights ranging from 62 to 68 inches. Now, using the 1.5IQR rule, we can identify potential outliers. Any height less than 62 - 1.5(6) or greater than 68 + 1.5*(6) is considered an outlier. This translates to heights below 46 inches or above 82 inches.
By applying the IQR and its associated rule, we’ve quickly identified the extreme heights in our dataset, providing valuable insights into the distribution of heights among these individuals.
Limitations and Considerations
While IQR is a powerful tool, it is not without its limitations. It is most effective when dealing with relatively large datasets, as it may not capture the spread accurately in smaller datasets. Additionally, IQR is sensitive to extreme values, so if the dataset contains many outliers, it may not provide an accurate representation of the data’s spread.
In conclusion, the Interquartile Range is a vital statistic in the analyst’s toolkit, offering a quick and effective way to understand data distribution and variability. By grasping the concept of IQR and its applications, researchers and analysts can make more informed decisions, identify outliers, and gain deeper insights into their datasets.
Understanding and applying IQR can revolutionize the way you interpret data, providing a clearer picture of its distribution and variability.
Frequently Asked Questions
How is IQR different from the standard deviation or range?
+IQR differs from standard deviation and range in its focus and robustness. While standard deviation measures the average distance of data points from the mean, IQR focuses on the spread of the middle 50% of the data. This makes IQR less sensitive to extreme values and more effective in identifying outliers. Similarly, the range, which is the difference between the maximum and minimum values, can be influenced by outliers, whereas IQR provides a more stable measure of variability.
Can IQR be negative?
+No, IQR cannot be negative. Since it represents the difference between the third quartile and the first quartile, both of which are values within the dataset, the result will always be positive or zero. A negative IQR would indicate that the lower half of the data is greater than the upper half, which is statistically impossible.
What is the 1.5*IQR rule used for, and why is it effective?
+The 1.5*IQR rule is a commonly used method for identifying outliers. It is effective because it provides a conservative yet robust threshold for outlier detection. By setting the threshold at 1.5 times the IQR, we ensure that only the most extreme values, which are likely to be true outliers, are flagged. This approach strikes a balance between capturing genuine outliers and avoiding false positives, making it a reliable tool for data analysis.
Are there any alternative methods for calculating IQR?
+Yes, there are alternative methods for calculating IQR, particularly in situations where the dataset is not ordered or the quartiles are not known. One common approach is to use the median of the absolute deviations (MAD) of the data points from the median. This method, while slightly more complex, provides a robust estimate of IQR, especially in datasets with outliers.



