4 Ways to Find Significance in Excel

Data analysis is an integral part of many industries and research fields, and Microsoft Excel has long been a go-to tool for professionals and academics alike. One crucial aspect of data analysis is determining statistical significance, which helps us make informed decisions and draw meaningful conclusions from our data. In this article, we will explore four methods to find significance in Excel, providing a comprehensive guide for data analysts and enthusiasts.
Understanding Significance in Excel

Before diving into the methods, let’s clarify what we mean by “significance” in the context of Excel. In statistical analysis, significance refers to the probability that a result or observation is not due to chance alone. It helps us determine whether the patterns or relationships we observe in our data are meaningful or merely random fluctuations.
Excel offers a range of tools and functions to calculate significance, making it an invaluable resource for data-driven decision-making. By understanding and utilizing these methods, we can gain deeper insights from our datasets and make more accurate predictions.
Method 1: Hypothesis Testing with the T.TEST Function
One of the most common ways to determine significance in Excel is through hypothesis testing. The T.TEST function is a powerful tool that allows us to compare two sets of data and assess whether the means of these datasets are significantly different. This method is particularly useful when we want to understand the relationship between two variables or when we have a specific research question to answer.
The T.TEST function takes into account various factors, such as the sample size, the means of the datasets, and the significance level (often denoted as α). It then calculates a p-value, which represents the probability of observing the data if the null hypothesis (the assumption that there is no significant difference) is true.
To use the T.TEST function, follow these steps:
- Select the cell where you want the p-value to be displayed.
- Enter the formula =T.TEST(array1, array2, tails, type), where array1 and array2 are the ranges of data you want to compare, tails specifies whether you want a one-tailed or two-tailed test (usually set to 2 for a two-tailed test), and type determines the type of t-test to perform (typically set to 2 for a standard t-test).
- Press Enter, and Excel will calculate the p-value, indicating the significance of the difference between the two datasets.
A p-value less than the significance level (α) indicates that the difference between the means is statistically significant. In such cases, we can reject the null hypothesis and conclude that the datasets are indeed different.
Example: Comparing Sales Performance
Imagine you are a marketing analyst, and you want to compare the sales performance of two different advertising campaigns. You have data on the sales generated by each campaign, and you suspect that one campaign might be more effective than the other.
| Campaign A Sales | Campaign B Sales |
|---|---|
| 120 | 150 |
| 110 | 135 |
| 130 | 160 |
| 105 | 145 |
Using the T.TEST function, you can determine whether the difference in sales performance is statistically significant. If the p-value is less than your chosen significance level, you can conclude that one campaign significantly outperforms the other.
Method 2: ANOVA (Analysis of Variance) with the ANOVA Function
When dealing with more than two datasets, the ANOVA (Analysis of Variance) method becomes a powerful tool for finding significance. ANOVA allows us to compare the means of multiple groups and determine if they are significantly different from each other.
Excel's ANOVA function provides a comprehensive way to perform this analysis. It calculates the F-statistic and the corresponding p-value, which helps us assess the significance of the differences between the means.
To use the ANOVA function in Excel, follow these steps:
- Select the cell where you want the ANOVA results to be displayed.
- Enter the formula =ANOVA(array1, array2, ...), where array1, array2, etc. are the ranges of data for each group you want to compare.
- Press Enter, and Excel will provide you with an ANOVA table, including the F-statistic and the p-value.
If the p-value is less than the significance level (α), it indicates that at least one of the group means is significantly different from the others. This method is particularly useful when dealing with multiple datasets and trying to identify patterns or differences.
Example: Comparing Exam Scores
Suppose you are a teacher, and you want to compare the exam scores of three different study groups. You suspect that the teaching methods or study materials might have an impact on the students’ performance.
| Group 1 Scores | Group 2 Scores | Group 3 Scores |
|---|---|---|
| 85 | 90 | 80 |
| 78 | 88 | 85 |
| 92 | 82 | 75 |
| 80 | 95 | 88 |
By using the ANOVA function, you can determine if the mean scores of these three groups are significantly different. If the p-value is significant, you can conclude that the teaching methods or materials had a measurable impact on the students' exam performance.
Method 3: Correlation Analysis with the CORREL Function
Correlation analysis is a valuable method for understanding the relationship between two continuous variables. It helps us determine if and how strongly two variables are related to each other. Excel’s CORREL function calculates the correlation coefficient, which ranges from -1 to 1, indicating the strength and direction of the relationship.
To use the CORREL function, follow these steps:
- Select the cell where you want the correlation coefficient to be displayed.
- Enter the formula =CORREL(array1, array2), where array1 and array2 are the ranges of data for the two variables you want to analyze.
- Press Enter, and Excel will calculate the correlation coefficient, indicating the strength of the relationship between the variables.
A correlation coefficient close to 1 indicates a strong positive relationship, while a coefficient close to -1 suggests a strong negative relationship. A coefficient close to 0 indicates little to no relationship between the variables.
Example: Studying Sleep and Exam Performance
Let’s say you are a researcher interested in understanding the relationship between sleep duration and exam performance. You collect data on the sleep hours and exam scores of a group of students.
| Sleep Hours | Exam Score |
|---|---|
| 7 | 85 |
| 6 | 78 |
| 8 | 92 |
| 9 | 90 |
| 5 | 72 |
By using the CORREL function, you can calculate the correlation coefficient between sleep hours and exam scores. If the coefficient is significantly different from 0, it suggests a relationship between sleep duration and exam performance. Further analysis would be required to determine the nature and strength of this relationship.
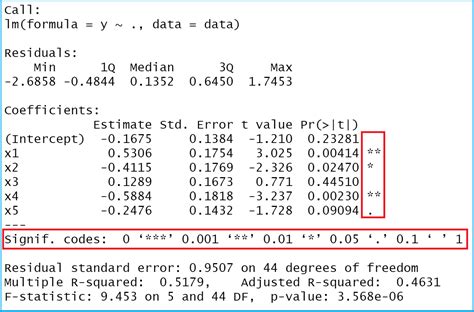
Method 4: Regression Analysis with the LINEST Function

Regression analysis is a powerful technique for understanding the relationship between a dependent variable and one or more independent variables. It helps us make predictions and understand the impact of various factors on an outcome. Excel’s LINEST function is a versatile tool for performing linear regression analysis.
The LINEST function calculates various statistics, including the slope and intercept of the regression line, as well as the R-squared value, which indicates the proportion of the variation in the dependent variable that can be explained by the independent variables.
To use the LINEST function, follow these steps:
- Select the cells where you want the regression statistics to be displayed.
- Enter the formula =LINEST(known_y's, known_x's, const, stats), where known_y's and known_x's are the ranges of data for the dependent and independent variables, const specifies whether to force the regression line to pass through the origin (usually set to FALSE), and stats determines whether additional statistics are included in the results (typically set to TRUE for a comprehensive analysis).
- Press Enter, and Excel will provide you with a range of regression statistics, including the slope, intercept, and R-squared value.
The slope of the regression line indicates the change in the dependent variable for a one-unit change in the independent variable. The intercept represents the value of the dependent variable when all independent variables are zero. The R-squared value provides insight into how well the regression model fits the data.
Example: Predicting Housing Prices
Imagine you are a real estate analyst, and you want to predict housing prices based on various factors such as square footage, number of bedrooms, and location. You have historical data on these variables and the corresponding housing prices.
| Square Footage | Bedrooms | Location | Price |
|---|---|---|---|
| 1500 | 3 | Suburb | $300,000 |
| 2000 | 4 | City Center | $450,000 |
| 1200 | 2 | Suburb | $220,000 |
| 1800 | 3 | City Center | $400,000 |
| 1000 | 2 | Suburb | $180,000 |
By using the LINEST function, you can perform a regression analysis to determine the impact of square footage, number of bedrooms, and location on housing prices. The slope and intercept values will provide insights into the relationship, and the R-squared value will indicate how well the model predicts housing prices.
Conclusion
Excel offers a plethora of tools and functions to find significance in data analysis. Whether you’re performing hypothesis testing, ANOVA, correlation analysis, or regression analysis, Excel provides the means to make informed decisions and draw meaningful conclusions from your data. By understanding and utilizing these methods, you can unlock the power of statistical analysis and gain valuable insights from your datasets.
Frequently Asked Questions
How do I choose the appropriate significance level (α) for my analysis?
+The choice of significance level depends on the field and the specific requirements of your analysis. In many fields, a significance level of 0.05 (5%) is commonly used, indicating that there is a 5% chance of rejecting the null hypothesis when it is true. However, in certain fields or for more conservative analyses, a lower significance level like 0.01 (1%) might be preferred.
What if my data does not meet the assumptions of ANOVA or regression analysis?
+If your data does not meet the assumptions of ANOVA or regression analysis, such as normality or equal variance, you might need to consider alternative methods. Transforming the data or using non-parametric tests can be options. It’s important to consult statistical references or seek advice from experts to choose the most appropriate method for your data.
How do I interpret the p-value obtained from hypothesis testing or ANOVA?
+The p-value represents the probability of observing the data (or more extreme data) if the null hypothesis is true. If the p-value is less than the chosen significance level, it suggests that the null hypothesis can be rejected, and the observed difference or relationship is statistically significant. Conversely, a p-value greater than the significance level indicates that the null hypothesis cannot be rejected.
Can I perform multiple regression analysis in Excel?
+Yes, Excel supports multiple regression analysis. The LINEST function can handle multiple independent variables by providing an array of known_x’s. This allows you to analyze the impact of multiple factors on a dependent variable simultaneously. Excel provides the necessary statistics to interpret the results of multiple regression.



