Mastering Relative Frequency: 3 Easy Steps
Welcome to the world of statistics, where data analysis is key to understanding and interpreting various phenomena. One of the fundamental concepts in statistics is relative frequency, a measure that allows us to quantify the likelihood of an event occurring relative to the total number of outcomes. In this comprehensive guide, we will explore the concept of relative frequency and provide you with three simple steps to master its calculation and interpretation.
Understanding Relative Frequency

Relative frequency is a statistical term used to describe the proportion of times a particular outcome occurs in relation to the total number of outcomes. It is often expressed as a decimal or a percentage and provides valuable insights into the likelihood of an event. Relative frequency is particularly useful when dealing with large datasets or when we want to compare the probabilities of different events.
Imagine you are analyzing the results of a survey where participants were asked about their preferred method of transportation. The survey collected responses from 1000 participants, and you are interested in understanding the relative frequency of each transportation choice. By calculating the relative frequency, you can determine which mode of transportation is most popular among the respondents.
Step 1: Collect and Organize Data

The first step in mastering relative frequency is to collect and organize your data systematically. This step is crucial as it sets the foundation for accurate analysis. Here’s how you can effectively collect and organize your data:
- Define Your Variables: Clearly define the variables you want to analyze. In our transportation survey example, the variables could be "Walking," "Biking," "Public Transport," and "Driving." Ensure that your variables are mutually exclusive and collectively exhaustive to capture all possible outcomes.
- Gather Data: Collect data from a representative sample or the entire population, depending on your study's scope. In our case, you would gather responses from the 1000 participants in the survey.
- Organize Data: Create a table or a spreadsheet to record the data. Each row could represent an individual's response, and the columns could be labeled with the defined variables. This organization will make it easier to count the occurrences of each outcome.
| Participant ID | Transportation Choice |
|---|---|
| P1 | Walking |
| P2 | Public Transport |
| P3 | Driving |
| ... | ... |
| P1000 | Biking |
Step 2: Calculate Relative Frequency
Once you have organized your data, it’s time to calculate the relative frequency for each outcome. This step involves simple arithmetic and provides a quantitative measure of the likelihood of each event.
Formula for Relative Frequency
The formula for calculating relative frequency is straightforward:
Relative Frequency = (Number of Times an Outcome Occurs) / (Total Number of Outcomes)
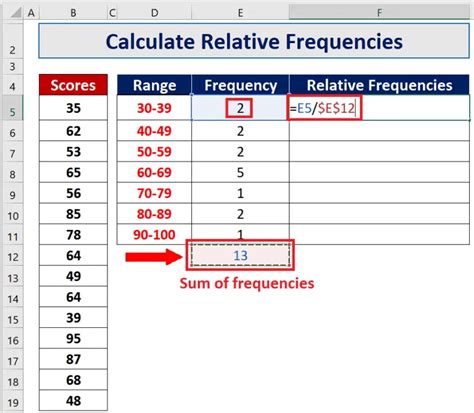
In our transportation survey example, let's assume the data shows that "Walking" occurred 250 times, "Biking" occurred 150 times, "Public Transport" occurred 300 times, and "Driving" occurred 300 times. We can calculate the relative frequency for each outcome as follows:
| Transportation Choice | Number of Occurrences | Relative Frequency |
|---|---|---|
| Walking | 250 | 0.25 (or 25%) |
| Biking | 150 | 0.15 (or 15%) |
| Public Transport | 300 | 0.30 (or 30%) |
| Driving | 300 | 0.30 (or 30%) |
From the calculations above, we can see that "Public Transport" and "Driving" have the same relative frequency of 0.30 (or 30%), indicating that they are equally likely outcomes according to our survey data.
Step 3: Interpret and Visualize Results
Interpreting and visualizing your calculated relative frequencies is essential to communicate your findings effectively. This step allows you to draw meaningful conclusions and make data-driven decisions.
Interpreting Relative Frequency
When interpreting relative frequency, consider the following:
- Probability Interpretation: Relative frequency can be interpreted as a probability. For example, a relative frequency of 0.30 for "Public Transport" means there is a 30% chance that a randomly selected participant prefers public transport.
- Comparison: Relative frequencies allow you to compare the likelihood of different events. In our survey, we can see that "Walking" is the least preferred option with a relative frequency of 0.25, while "Public Transport" and "Driving" are the most popular choices.
- Contextual Understanding: Relative frequency should be interpreted in the context of your study. Consider external factors, sample size, and other relevant variables that might influence the outcomes.
Visualizing Relative Frequency
Visual representations can greatly enhance the understanding and communication of your results. Here are some visualization techniques you can use:
- Bar Charts: Create a bar chart where the x-axis represents the different outcomes, and the y-axis represents the relative frequency. This visual representation makes it easy to compare the likelihood of each event.
- Pie Charts: Pie charts are another effective way to visualize relative frequencies. Each slice of the pie represents an outcome, and the size of the slice corresponds to its relative frequency. Pie charts are excellent for showing the proportion of each outcome.
- Frequency Tables: Present your calculated relative frequencies in a frequency table, as shown earlier. This table provides a concise summary of your findings and allows for easy reference.
Advanced Considerations

While the three steps outlined above provide a solid foundation for mastering relative frequency, there are some advanced considerations to keep in mind, especially when dealing with more complex datasets or advanced statistical analyses.
Confidence Intervals
When working with relative frequencies based on sample data, it’s important to consider the concept of confidence intervals. Confidence intervals provide a range of values within which we can estimate the true population relative frequency with a certain level of confidence (e.g., 95% confidence interval). This consideration is particularly relevant when making inferences about a larger population based on a sample.
Margin of Error
In survey-based research, the concept of margin of error is crucial. The margin of error represents the maximum difference between the true population relative frequency and the estimated relative frequency based on the sample. It takes into account factors such as sample size and variability in the data. Understanding the margin of error helps in making more accurate interpretations and decisions.
Statistical Significance
When comparing relative frequencies between different groups or conditions, it’s essential to determine whether the differences are statistically significant. Statistical significance tests, such as chi-square tests or t-tests, can help determine if the observed differences are likely due to chance or if they represent a genuine difference in the underlying populations.
Conclusion
Mastering relative frequency is a valuable skill in the field of statistics, allowing us to quantify and compare the likelihood of events. By following the three simple steps outlined in this guide—collecting and organizing data, calculating relative frequency, and interpreting and visualizing results—you can effectively analyze and communicate your findings. Remember to consider advanced concepts like confidence intervals, margin of error, and statistical significance when working with more complex datasets or making inferences about larger populations.
What is the difference between relative frequency and probability?
+Relative frequency and probability are closely related concepts, but they have subtle differences. Relative frequency is a measure of how often an event occurs relative to the total number of outcomes, while probability is a measure of the likelihood of an event occurring. Probability is often expressed as a number between 0 and 1 or as a percentage, and it represents the theoretical or long-term likelihood of an event. Relative frequency, on the other hand, is based on observed data and is a measure of the actual frequency of an event occurring in a specific sample or dataset.
Can relative frequency values exceed 1 or be negative?
+No, relative frequency values should always be between 0 and 1, inclusive. Since relative frequency represents the proportion of occurrences relative to the total, it cannot exceed 1, as this would imply more occurrences than the total. Similarly, relative frequency cannot be negative, as it represents a count of occurrences, which is always a non-negative number.
How does relative frequency help in decision-making?
+Relative frequency provides valuable insights that aid in decision-making by quantifying the likelihood of different outcomes. It allows stakeholders to assess the potential impact of various choices and make informed decisions based on data. For example, in business, relative frequency can help determine the popularity of different products, guiding marketing strategies and resource allocation.



