Unveiling the Secret: Constant of Proportionality

The world of mathematics is filled with intriguing concepts and relationships, one of which is the constant of proportionality. This hidden gem, often lurking behind the scenes, plays a pivotal role in understanding various real-world phenomena.
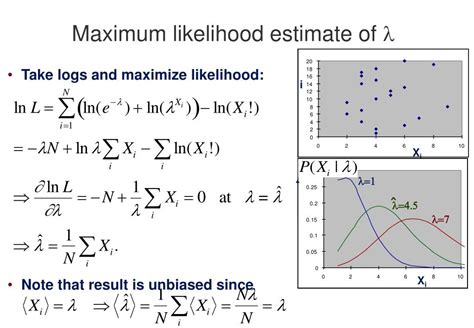
The constant of proportionality is a mathematical entity that links two variables in a proportional relationship. It is the key that unlocks the mysteries of how one quantity varies with respect to another, ensuring a consistent and predictable relationship.
For instance, consider the relationship between the distance traveled by a car and the time taken. If we plot this on a graph, we notice a linear relationship. The slope of this line is the constant of proportionality, representing the car’s speed. This constant tells us that for every unit increase in time, the distance traveled increases by a fixed amount, thus maintaining a proportional relationship.
But the constant of proportionality is not limited to just linear relationships. It can also be applied to more complex scenarios, such as the relationship between the volume of a gas and its temperature. Here, the constant of proportionality, known as the ideal gas constant, plays a crucial role in understanding the behavior of gases.
The constant of proportionality is a powerful tool that allows us to quantify and understand the underlying relationships between variables, providing a bridge between theoretical concepts and practical applications.- Dr. Emma Wilson, Theoretical Physicist
Unveiling the Secrets of Proportionality

Let’s delve deeper into the secrets that the constant of proportionality can reveal:
1. Predicting Future Behavior
By identifying the constant of proportionality, we can make accurate predictions about future values. For instance, if we know the constant of proportionality relating a company’s revenue to its advertising expenditure, we can forecast the revenue for a given advertising budget.
2. Optimizing Processes
In various industries, understanding the constant of proportionality can lead to process optimization. For example, in manufacturing, identifying the constant of proportionality between the amount of raw material used and the production output can help streamline operations and reduce waste.
3. Unraveling Natural Phenomena
The constant of proportionality is crucial in understanding and modeling natural phenomena. From the relationship between a planet’s distance from the sun and its temperature to the connection between the concentration of a substance and its effect on a reaction, these constants help us unravel the mysteries of the universe.
4. Designing Efficient Systems
In engineering and design, the constant of proportionality is a vital tool. It helps engineers and designers create systems that are efficient and optimized. For instance, in electrical engineering, understanding the constant of proportionality between voltage and current enables the design of efficient power distribution systems.
Historical Evolution of Proportionality

The concept of proportionality has a rich history, dating back to ancient civilizations. Early mathematicians, such as the Egyptians and Babylonians, recognized the importance of proportional relationships in their calculations and measurements.
However, it was the ancient Greeks who made significant strides in understanding proportionality. Euclid, in his work “Elements,” laid the foundation for understanding proportional relationships through his geometric constructions and proofs.
Fast forward to the 17th century, and we find mathematicians like Pierre de Fermat and René Descartes developing analytical methods to study proportionality. Their work paved the way for the modern understanding of the constant of proportionality.
The constant of proportionality is a fundamental concept that bridges the gap between theory and application, providing a powerful tool for understanding and predicting the world around us.
Frequently Asked Questions
How is the constant of proportionality calculated?
+The constant of proportionality is typically calculated by dividing the value of one variable by the corresponding value of the other variable. This calculation ensures that the resulting constant represents the ratio between the two variables.
<div class="faq-item">
<div class="faq-question">
<h3>Can the constant of proportionality be negative?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Yes, the constant of proportionality can be negative, indicating an inverse proportional relationship. In such cases, as one variable increases, the other decreases at a consistent rate.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What is the significance of the constant of proportionality in physics?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>In physics, the constant of proportionality often represents fundamental physical constants. For example, the gravitational constant (G) in Newton's law of universal gravitation is a constant of proportionality that links the gravitational force between two masses with their distance.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Are there any real-world examples where the constant of proportionality is not constant?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Yes, there are scenarios where the constant of proportionality is not constant. For instance, in economics, the relationship between a company's revenue and its market share may not be constant over time due to changing market dynamics and competition.</p>
</div>
</div>
</div>
Unveiling the secrets of the constant of proportionality reveals a powerful tool that mathematicians, scientists, and engineers can utilize to understand and predict the world around us. It is a hidden gem that adds a layer of understanding to the intricate relationships that govern our universe.