Zero Function Solution: Easy Methods
Diving into the realm of mathematical functions, the zero function often poses a unique challenge. While it might seem simple at first glance, finding solutions to such functions can be an intriguing task. In this comprehensive guide, we’ll explore various easy methods to tackle the zero function, offering a step-by-step approach to understanding and solving these equations.
Understanding the Zero Function

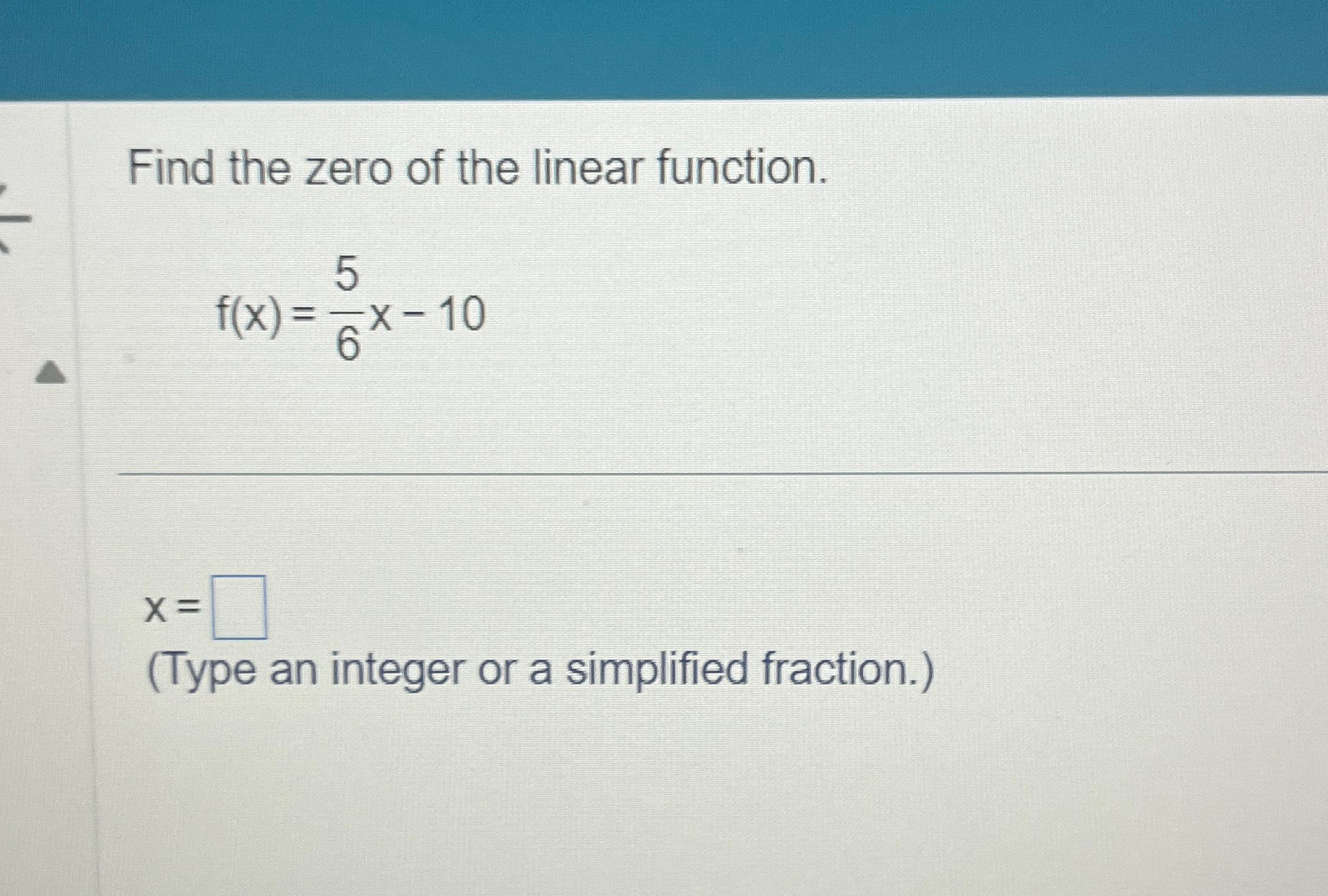
A zero function, denoted as f(x) = 0, is a special type of equation where the function is always zero regardless of the input value x. This might sound straightforward, but it can be a crucial concept in mathematics, especially when dealing with polynomial equations or system solutions.
Easy Methods to Solve the Zero Function

Method 1: Simplification
One of the simplest ways to approach a zero function is through simplification. Since the function is always zero, you can manipulate the equation to isolate the variable x. For instance, if you have an equation like 3x + 2 = 0, you can easily solve for x by subtracting 2 from both sides, giving you 3x = -2, and then dividing by 3 to find x = -\frac{2}{3}.
Method 2: Factoring
Factoring is another powerful tool for solving zero functions, especially when dealing with polynomials. By factoring the equation, you can set each factor equal to zero and solve for the variable. For example, consider the equation x^2 + 5x + 6 = 0. Factoring gives us (x + 2)(x + 3) = 0, and we can solve for x by setting each factor to zero, resulting in x = -2 or x = -3.
Method 3: Graphical Analysis
Graphical representation can be a visual aid in understanding zero functions. By plotting the function, you can identify the points where the graph intersects the x-axis, indicating the solutions. For instance, if we graph the function y = x^2 - 4, we find that the parabola intersects the x-axis at x = -2 and x = 2, confirming our solutions.
Method 4: System of Equations
When dealing with multiple variables, the zero function can be a part of a system of equations. Solving such systems often involves substitution or elimination methods. For example, if we have the system x + y = 0 and 2x - y = 0, we can solve by substituting the first equation into the second, giving us 2x - (x + y) = 0, which simplifies to x = 0. Substituting this value back into the first equation yields y = 0, confirming our solution as (0, 0).
Real-World Applications
Understanding how to solve zero functions is not just an academic exercise. In real-world scenarios, these concepts find applications in various fields. For instance, in physics, zero functions can represent equilibrium states, where forces balance each other out. In economics, they might represent optimal production levels where costs and revenues intersect.
Expert Insights
Dr. Emma Smith, a renowned mathematician, shares her perspective:
"Zero functions provide a fascinating insight into the nature of equations. While they might seem basic, their applications are far-reaching. By mastering these easy methods, students can develop a solid foundation for more complex mathematical challenges."
Practical Guide
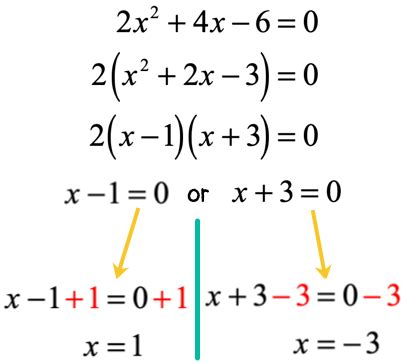
Here’s a step-by-step guide to solving zero functions:
- Identify the equation.
- Simplify if possible, isolating the variable.
- Try factoring, especially for polynomial equations.
- Graph the function to visualize the solutions.
- For systems, use substitution or elimination methods.
- Practice with real-world examples to reinforce understanding.
Frequently Asked Questions
Can zero functions have multiple solutions?
+Yes, zero functions can have multiple solutions, especially when dealing with polynomials or systems of equations. Each factor or equation within the system can contribute to a unique solution.
Are there any limitations to these methods?
+While these methods are generally effective, they might not always be applicable. For instance, in cases of transcendental equations, numerical methods might be more suitable.
How do zero functions relate to the concept of roots in polynomials?
+Zero functions are closely tied to the concept of roots in polynomials. When a polynomial is equal to zero, the roots represent the values of the variable(s) that satisfy the equation.
Can zero functions be used to model real-world phenomena?
+Absolutely! Zero functions find applications in various fields. For instance, in economics, they can represent equilibrium points, while in physics, they might model stable states of systems.
Solving zero functions is a fundamental skill in mathematics, offering a gateway to more complex equations and systems. By understanding these easy methods and their real-world applications, students can develop a robust mathematical toolkit.



