Mastering Quadratic Equation Factoring: 5 Tips
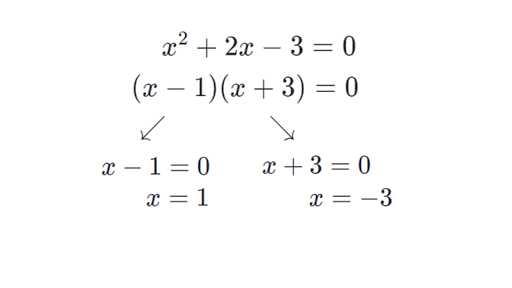
Unlocking the Secrets of Quadratic Equation Factoring

Factoring quadratic equations is a fundamental skill in mathematics, one that unlocks a deeper understanding of algebraic concepts. While it may seem daunting at first, with the right techniques and a systematic approach, you can become a master at solving these equations. Here are five essential tips to help you conquer quadratic equation factoring and unlock the mysteries of algebra.
1. Understand the Basics: A Solid Foundation
Before diving into the world of factoring, ensure you have a strong grasp of the fundamental concepts. Quadratic equations, typically in the form of ax^2 + bx + c = 0, where a, b, and c are coefficients, can be factored into two linear binomials. This process involves breaking down the quadratic into simpler expressions, which can then be solved individually.
To begin, refresh your memory on the basics of quadratic equations:
- The standard form: ax^2 + bx + c = 0, where a, b, and c are integers.
- The zero product property: If ab = 0, then either a = 0 or b = 0.
- The FOIL method: A useful technique for multiplying binomials.
Having a solid foundation in these concepts will make factoring quadratics a more intuitive process.
2. Identify the Right Factors: A Key to Success
Factoring quadratics often involves trial and error, but with a strategic approach, you can minimize the guesswork. One effective strategy is to identify the factors of the coefficients a and c. These factors will give you clues about the possible binomials that can be multiplied to form the quadratic.
For example, consider the quadratic x^2 + 5x + 6 = 0. The factors of 6 (the coefficient of c) are 1, 2, 3, and 6. By pairing these factors, you can identify potential binomials: (x + 1)(x + 6), (x + 2)(x + 3), etc. This approach significantly narrows down the possibilities, making the factoring process more efficient.
3. Use the Zero Product Property: A Powerful Tool
The zero product property is a powerful tool in factoring quadratics. This property states that if ab = 0, then either a = 0 or b = 0 (or both). In the context of quadratic equations, this means that if the product of two binomials is zero, then at least one of the binomials must be equal to zero.
For instance, in the equation x^2 - 4x + 4 = 0, you can apply the zero product property to identify the possible factors. Since 4 is a perfect square, you can try factoring it as (x - 2)(x - 2), which yields x - 2 = 0 or x - 2 = 0, leading to the solutions x = 2 and x = 2.
4. Practice with Different Types of Quadratics
Quadratic equations come in various forms, and practicing with a wide range of examples is crucial to mastering factoring. Here are some common types to consider:
- Monic quadratics: These have a leading coefficient of 1, such as x^2 + 5x + 6 = 0.
- Quadratics with a leading coefficient of 2 or more: For example, 2x^2 + 7x - 3 = 0.
- Quadratics with a negative leading coefficient: Like -x^2 + 3x + 2 = 0.
- Quadratics with fractional coefficients: Such as (1⁄2)x^2 + 3x + 2 = 0.
Practicing with different types of quadratics will help you develop a versatile skill set and enhance your problem-solving abilities.
5. Visualize the Graph: A Graphical Perspective
While factoring is primarily an algebraic process, a graphical perspective can provide valuable insights. The graph of a quadratic equation, a parabola, can give you clues about the solutions.
For instance, if the quadratic has a positive leading coefficient, the parabola opens upward, indicating that the solutions are both positive or both negative. Conversely, if the leading coefficient is negative, the parabola opens downward, suggesting that the solutions have opposite signs.
By analyzing the graph, you can gain a deeper understanding of the quadratic equation and its solutions, making the factoring process more intuitive.
Conclusion: A Journey to Mathematical Mastery

Mastering quadratic equation factoring is a journey that requires patience, practice, and a systematic approach. By understanding the basics, identifying the right factors, utilizing the zero product property, practicing with diverse examples, and adopting a graphical perspective, you can become adept at solving these equations.
Remember, mathematics is a language, and quadratic equation factoring is one of its most elegant expressions. With dedication and the right techniques, you can unlock the secrets of algebra and become a true master of quadratic equations.
Happy factoring!