Excel's Guide to Two-Factor ANOVA
Excel's Comprehensive Guide: Unlocking the Power of Two-Factor Analysis of Variance (ANOVA)

In the realm of statistical analysis, the Analysis of Variance (ANOVA) stands as a cornerstone technique, offering insights into the impact of multiple factors on a given outcome. While the one-factor ANOVA is a common starting point, it's the two-factor ANOVA that unlocks more nuanced and complex insights. In this comprehensive guide, we will delve into the world of two-factor ANOVA, utilizing the powerful tool of Excel. By the end, you'll not only grasp the theoretical underpinnings but also master the practical application of this statistical powerhouse.
For those familiar with one-factor ANOVA, the concept of two-factor ANOVA might seem like a logical next step. However, the power of two-factor ANOVA lies in its ability to analyze the effects of two independent variables (factors) on a single dependent variable. This makes it an invaluable tool for researchers, data analysts, and professionals across various fields, from scientific experiments to market research.
Imagine you're a researcher studying the impact of different teaching methods (Factor A) and study materials (Factor B) on student performance (the dependent variable). The two-factor ANOVA allows you to analyze the main effects of each factor as well as the interaction effect, providing a comprehensive understanding of the data.
Let's embark on this journey, exploring the theory, practical application, and real-world implications of two-factor ANOVA in Excel. By the end, you'll be equipped with the knowledge and skills to confidently tackle complex statistical analyses and draw meaningful conclusions from your data.
Understanding the Theory: A Deep Dive into Two-Factor ANOVA

At its core, the two-factor ANOVA is a statistical method used to determine the impact of two independent variables (factors) on a single dependent variable. It is an extension of the one-way ANOVA, which analyzes the effect of a single factor on the dependent variable. The two-factor ANOVA, also known as a two-way ANOVA, allows us to delve deeper into the relationship between factors and their interaction.
The theoretical foundation of two-factor ANOVA rests on the principles of statistical inference and hypothesis testing. We start with the null hypothesis, which assumes that there is no significant difference between the means of the dependent variable across the levels of the two factors. Our goal is to collect and analyze data to either accept or reject this null hypothesis.
Let's break down the key components of a two-factor ANOVA:
- Factors (Independent Variables): In a two-factor ANOVA, we have two independent variables, often denoted as Factor A and Factor B. These factors represent the variables we believe may influence the dependent variable.
- Levels of Factors: Each factor has multiple levels or categories. For instance, Factor A might have three levels (A1, A2, and A3), while Factor B might have two levels (B1 and B2). These levels represent the different conditions or treatments within each factor.
- Dependent Variable: This is the variable we are interested in measuring and understanding its relationship with the two factors. It is the outcome or response variable that we want to explain or predict.
- Interaction Effect: One of the critical aspects of two-factor ANOVA is the interaction effect. This occurs when the impact of one factor on the dependent variable depends on the level of the other factor. In other words, the effect of Factor A on the dependent variable may vary depending on the level of Factor B, and vice versa.
To illustrate the concept of interaction effect, consider an example in agricultural research. You're studying the effect of two fertilizers (Factor A) and two soil types (Factor B) on crop yield (the dependent variable). The interaction effect would reveal whether the effectiveness of a particular fertilizer depends on the soil type and vice versa.
The two-factor ANOVA helps us disentangle these complex relationships, providing a comprehensive understanding of how the factors and their interaction influence the dependent variable. By the end of this section, you'll have a solid grasp of the theoretical underpinnings, allowing you to move on to the practical application with confidence.
Practical Application: Excel's Two-Factor ANOVA in Action
Now that we've established the theoretical framework, let's dive into the practical side of two-factor ANOVA using Excel. Excel, with its powerful data analysis tools, simplifies the process, making it accessible to professionals and researchers alike.
Step 1: Data Preparation
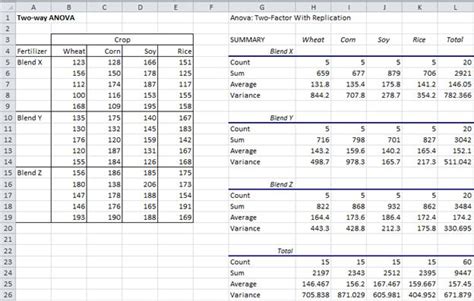
Before we begin our analysis, we need to ensure our data is properly organized. Here's an example dataset for a two-factor ANOVA:
| Factor A | Factor B | Dependent Variable |
|---|---|---|
| A1 | B1 | 25 |
| A1 | B2 | 30 |
| A2 | B1 | 28 |
| A2 | B2 | 32 |
| A3 | B1 | 22 |
| A3 | B2 | 29 |

In this dataset, we have three levels of Factor A and two levels of Factor B. The dependent variable represents the outcome of interest.
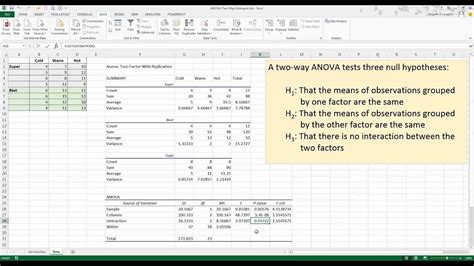
Step 2: Performing the Two-Factor ANOVA in Excel
- Open your Excel spreadsheet and ensure you have the Data Analysis ToolPak enabled. If not, go to the File tab, select Options, then Add-Ins, and enable the Analysis ToolPak.
- With your data selected, navigate to the Data tab and click on Data Analysis.
- Choose "ANOVA: Two-Factor With Replication" from the list of analysis tools.
- In the dialog box, specify your Input Range, ensuring it includes both factors and the dependent variable.
- Set the Alpha level (significance level) as desired (typically 0.05).
- Choose an Output Range or select New Worksheet Ply for the results.
- Click OK to initiate the analysis.
Excel will then generate a comprehensive report, including the sum of squares, degrees of freedom, mean squares, F-statistics, and p-values for each factor and the interaction effect.
Interpreting the Results
The ANOVA report provides a wealth of information. Let's break down the key components:
- Sum of Squares (SS): This measures the variation in the dependent variable attributed to each factor and the interaction effect.
- Degrees of Freedom (DF): Represents the number of independent pieces of information contributing to the analysis.
- Mean Squares (MS): Calculated by dividing the sum of squares by the degrees of freedom, it helps assess the variability explained by each factor.
- F-Statistics: Compares the mean squares of each factor and the interaction effect to the mean squares of the error (residual) term. A large F-statistic indicates a significant effect.
- P-Values: These values indicate the probability of observing the data if the null hypothesis is true. A small p-value suggests a significant effect.
By examining these results, we can make informed decisions about the significance of each factor and the interaction effect. If the p-value is below our chosen significance level (e.g., 0.05), we can reject the null hypothesis and conclude that the factor or interaction effect is statistically significant.
Visualizing the Results
To enhance our understanding, we can create visual representations of the data. Excel offers various charting options, such as box plots or line charts, to illustrate the effects of the factors and their interaction.
Real-World Applications and Implications
The power of two-factor ANOVA extends far beyond theoretical examples. Let's explore some real-world scenarios where this statistical technique proves invaluable.
Scenario 1: Medical Research
In medical research, two-factor ANOVA can be used to study the effectiveness of different treatments (Factor A) on patients with varying conditions (Factor B). For instance, researchers might examine the impact of two medications on patients with different stages of a disease.
Scenario 2: Marketing and Advertising
Marketers can utilize two-factor ANOVA to assess the effectiveness of advertising campaigns across different demographics (Factor A) and media channels (Factor B). This analysis helps identify the most successful combination of demographics and media channels for reaching target audiences.
Scenario 3: Environmental Science
Environmental scientists can apply two-factor ANOVA to study the impact of pollution levels (Factor A) on different species (Factor B) in an ecosystem. By analyzing the interaction effect, they can understand how species' responses to pollution vary.
Scenario 4: Sports Performance
In sports science, two-factor ANOVA can be used to evaluate the impact of training methods (Factor A) and dietary plans (Factor B) on athlete performance. This analysis helps coaches and athletes optimize their training regimens for peak performance.
Conclusion and Future Insights
The two-factor ANOVA is a powerful tool for unraveling the complex relationships between multiple factors and their impact on a dependent variable. By mastering this technique, professionals and researchers can make data-driven decisions with confidence. Excel, with its user-friendly interface and powerful analysis tools, simplifies the process, making statistical analysis accessible to a wide audience.
As we continue to explore the world of statistical analysis, the two-factor ANOVA serves as a foundation for more advanced techniques. The ability to analyze and interpret data using this method opens doors to a deeper understanding of the world around us. With the insights gained from two-factor ANOVA, we can make informed choices, drive innovation, and shape the future.
Whether you're a researcher, data analyst, or professional seeking to enhance your statistical skills, the journey into two-factor ANOVA is a rewarding one. Excel, with its versatility and user-friendly nature, is the perfect companion on this path. Embrace the power of statistical analysis, and let your data guide you towards meaningful insights and discoveries.
What is the difference between one-factor ANOVA and two-factor ANOVA?
+One-factor ANOVA analyzes the effect of a single independent variable (factor) on a dependent variable, while two-factor ANOVA extends this analysis to two independent variables, allowing for the examination of main effects and interaction effects.
How do I determine the significance of factors and interaction effects in two-factor ANOVA?
+The significance of factors and interaction effects is determined by comparing the p-values to the chosen significance level (typically 0.05). If the p-value is below the significance level, the factor or interaction effect is considered statistically significant.
Can I use two-factor ANOVA for non-numerical data?
+Two-factor ANOVA is primarily designed for numerical data. If you have non-numerical data, you may need to transform or categorize it into numerical form before conducting the analysis.