Unveiling the Mystery: Rotational Inertia Formula

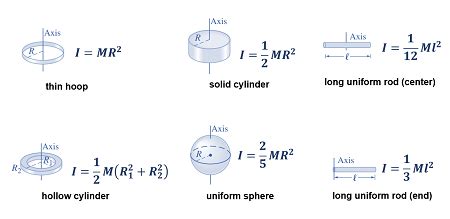
The concept of rotational inertia, often referred to as moment of inertia, is a fundamental principle in physics, offering profound insights into the dynamics of rotating objects. Understanding this concept is pivotal for scientists, engineers, and anyone intrigued by the physics governing rotational motion. This exploration delves into the core of rotational inertia, illuminating its mathematical intricacies and practical implications.

At its essence, rotational inertia quantifies an object’s resistance to changes in its rotational motion. Much like how mass resists changes in linear motion, rotational inertia is a measure of how an object resists changes in its angular velocity. This property is pivotal in comprehending the behavior of rotating systems, from celestial bodies to everyday mechanical devices.

The mathematical expression for rotational inertia is a cornerstone of this understanding. For a rigid body, the formula encapsulates the object’s mass distribution and its geometry relative to the axis of rotation. This equation serves as a vital tool for physicists and engineers, enabling precise calculations and predictions of rotational behavior.

In the following sections, we will embark on a comprehensive journey, unraveling the complexities of the rotational inertia formula. We will dissect its components, explore its applications, and highlight its significance in various domains. Through this exploration, we aim to provide a lucid and comprehensive understanding of this pivotal concept in physics.

Defining Rotational Inertia

Rotational inertia, symbolized by I in physics, represents an object’s propensity to resist changes in its rotational motion. It is akin to the concept of inertia in linear motion, but tailored to rotational dynamics. This property is intrinsic to every object and is determined by its mass distribution and the axis around which it rotates.

The fundamental formula for rotational inertia for a rigid body is expressed as:

\[ \begin{equation*} I = \sum_i m_i \cdot r_i^2 \end{equation*} \]

Here, I represents the moment of inertia, m_i signifies the mass of each particle or element of the object, and r_i denotes the perpendicular distance of that mass from the axis of rotation. This equation encapsulates the essence of rotational inertia, highlighting the influence of both mass and its distribution on an object’s rotational behavior.

Understanding the Components

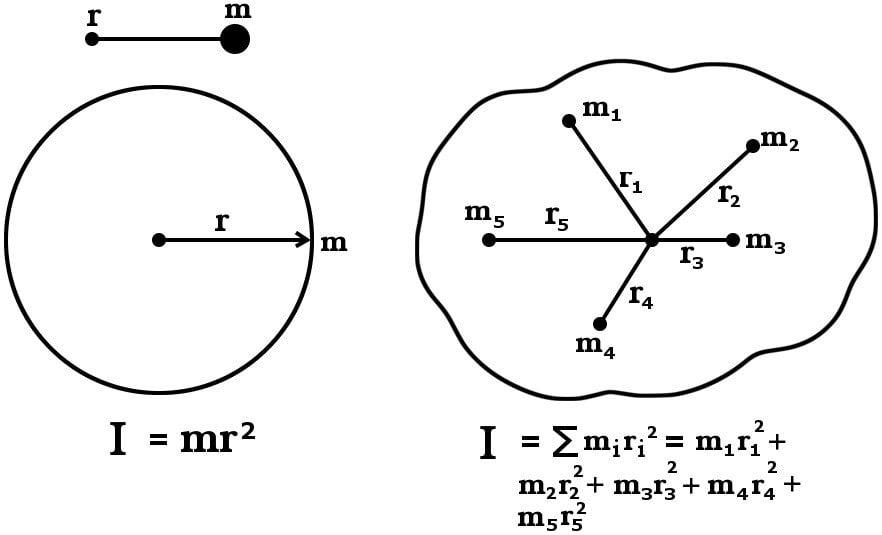
To grasp the rotational inertia formula, it is essential to dissect its components:

• Mass (m_i): The mass of each element or particle of the object. In physics, mass is a fundamental property, representing the amount of matter in an object. It is a key factor in determining an object’s resistance to changes in motion, whether linear or rotational.

• Distance from Axis (r_i): This parameter represents the perpendicular distance of each mass element from the axis of rotation. It plays a crucial role in the calculation of rotational inertia, as the distance from the axis influences the object’s rotational behavior.

Application in Real-World Scenarios

The rotational inertia formula finds extensive application across various fields, offering profound insights into the behavior of rotating systems:

Astronomy and Astrophysics

In the realm of astronomy, rotational inertia is pivotal in understanding the dynamics of celestial bodies. From the rotation of planets and moons to the spin of stars and galaxies, this principle governs their behavior. By applying the rotational inertia formula, scientists can predict and analyze the rotational characteristics of these cosmic entities.

For instance, the rotation of Earth on its axis, which gives rise to day and night, is governed by its rotational inertia. Similarly, the study of distant exoplanets and their rotation rates relies on this fundamental concept.

Engineering and Mechanics

Engineers and mechanics utilize the rotational inertia formula to design and optimize rotating machinery. Whether it’s a car’s wheels, a turbine’s blades, or a gyroscope’s spin, understanding rotational inertia is crucial for efficient and safe operation. By manipulating the mass distribution and geometry of rotating components, engineers can control their rotational behavior, enhancing performance and stability.

Consider the example of a gyroscope, a device that maintains its orientation due to its rotational inertia. This principle is fundamental in navigation systems, stabilization mechanisms, and even spacecraft control.

Sports and Athletics

In the world of sports, rotational inertia plays a subtle yet significant role. Consider the spin of a tennis ball, the rotation of a gymnast’s body, or the swing of a baseball bat. All these actions are influenced by the rotational inertia of the involved objects and bodies. By understanding this principle, athletes can optimize their performance and technique.

For instance, a tennis player can impart more spin to a ball by adjusting the angle and speed of their racket swing, leveraging the rotational inertia of the ball.

Historical Evolution of the Concept

The concept of rotational inertia has a rich historical evolution, dating back to the works of renowned physicists such as Isaac Newton and Leonhard Euler. In the 17th century, Newton laid the foundation for understanding rotational motion, but it was Euler who developed the mathematical framework for rotational inertia in the 18th century.

Euler’s work on the principle of moments and the calculation of rotational inertia was a significant advancement in physics. His contributions paved the way for a deeper understanding of rotational dynamics and its applications in various fields.

Modern Applications and Innovations

In the modern era, the applications of rotational inertia have expanded exponentially. With advancements in technology and engineering, the principles of rotational inertia find use in cutting-edge domains:

• Robotics and Automation: Rotational inertia is crucial in the design of robotic arms and automated systems. By optimizing the rotational behavior of these systems, engineers can enhance precision and efficiency.

• Renewable Energy: In the realm of renewable energy, such as wind turbines and hydroelectric generators, understanding rotational inertia is vital for optimizing power generation.

• Quantum Mechanics: Even in the microscopic world of quantum physics, rotational inertia plays a role. Quantum systems, such as atomic and molecular rotations, exhibit unique rotational behaviors that are governed by quantum principles and rotational inertia.

Practical Implications and Future Trends

The understanding and application of rotational inertia have profound implications across various domains. From enhancing the efficiency of mechanical systems to predicting the behavior of celestial bodies, this principle is a cornerstone of modern science and engineering.

Looking ahead, the future holds exciting possibilities for the application of rotational inertia. With ongoing advancements in technology and our understanding of the universe, the principles of rotational inertia will continue to evolve and find new applications.

Conclusion

In conclusion, the rotational inertia formula is a powerful tool that unlocks the mysteries of rotational motion. From the celestial scales of galaxies to the intricate rotations of microscopic particles, this principle governs the dynamics of our universe. By comprehending and applying this formula, scientists, engineers, and enthusiasts can unravel the complexities of rotational behavior, paving the way for advancements in various fields.

    <div class="faq-item">
        <div class="faq-question">
            <h3>How does rotational inertia differ from linear inertia?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Rotational inertia and linear inertia are both manifestations of an object's resistance to changes in motion, but they apply to different types of motion. Linear inertia pertains to an object's resistance to changes in linear velocity, while rotational inertia is specific to rotational motion, resisting changes in angular velocity.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can rotational inertia be changed or manipulated?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Yes, rotational inertia can be altered by changing the mass distribution or the geometry of an object relative to the axis of rotation. Engineers and designers often manipulate rotational inertia to optimize the performance of rotating systems, such as in the design of efficient machinery or sports equipment.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>What are some real-world examples of rotational inertia in action?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Rotational inertia is pervasive in our daily lives. Some examples include the spin of a top, the rotation of a car's wheels, the swing of a golf club, and the motion of a door on its hinges. In each case, the object's resistance to changes in rotational motion is governed by its rotational inertia.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>How does rotational inertia impact the stability of rotating systems?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Rotational inertia plays a crucial role in the stability of rotating systems. A higher rotational inertia tends to make a system more stable, as it resists changes in angular velocity. This principle is exploited in various applications, such as in the design of gyroscopes for navigation and stabilization.</p>
        </div>
    </div>
</div>