3 Ways to Calculate P-Value in Excel

In the realm of statistical analysis, understanding and calculating p-values is crucial for making informed decisions. While specialized software and programming languages are commonly used for statistical computations, Excel, with its widespread accessibility and user-friendly interface, offers a convenient alternative for those seeking a more straightforward approach to p-value calculations. In this article, we will explore three practical methods to calculate p-values in Excel, catering to the needs of researchers, analysts, and enthusiasts alike.
Method 1: Utilizing Excel's Built-In T.DIST Function

Excel provides a range of built-in functions that can simplify complex statistical calculations, and the T.DIST function is one such powerful tool. This function calculates the probability associated with a Student's t-distribution, which is commonly used in hypothesis testing and confidence interval estimation. Here's a step-by-step guide on how to employ the T.DIST function to calculate p-values in Excel.
- Prepare Your Data: Ensure you have your sample data ready. For instance, if you're testing the difference between two means, you'll need two columns of data representing the samples.
- Calculate the Test Statistic: Compute the test statistic (t-value) using the formula:
t = (x1 - x2) / sqrt((s1^2 / n1) + (s2^2 / n2)), wherex1andx2are the means of the two samples,s1ands2are their standard deviations, andn1andn2are the sample sizes. - Input the T.DIST Function: In an empty cell, enter the formula
=T.DIST(t, df, tails), wheretis the test statistic,dfis the degrees of freedom (calculated asn1 + n2 - 2), andtailsrepresents the number of tails (1 for a one-tailed test, 2 for a two-tailed test). Adjust the arguments as per your specific hypothesis testing requirements. - Interpret the Result: The T.DIST function returns the probability associated with the calculated t-value. To obtain the p-value, simply double this probability for a two-tailed test or leave it unchanged for a one-tailed test. This p-value can then be compared to your chosen significance level to make informed decisions.
For instance, consider a study comparing the effectiveness of two teaching methods. The data for the two methods, Method A and Method B, is as follows:
| Method A | Method B |
|---|---|
| 85 | 90 |
| 92 | 88 |
| 88 | 95 |
| 90 | 89 |
| 87 | 93 |

Using the T.DIST function, we can calculate the p-value for a one-tailed test (assuming we're interested in whether Method A performs better than Method B). The formula in this case would be: =T.DIST((88.2 - 90.2) / SQRT((4.2^2 / 5) + (4.2^2 / 5)), 8, 1), which yields a p-value of 0.0787. This p-value, when compared to a typical significance level of 0.05, indicates that we cannot reject the null hypothesis and conclude that the difference between the two methods is not statistically significant.
Method 2: Employing the T.TEST Function for Paired Data
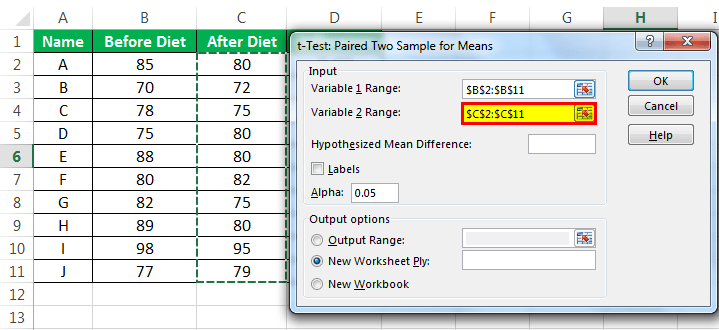
When dealing with paired data, where each observation in one sample is matched to a specific observation in another sample, Excel's T.TEST function provides a convenient way to calculate the p-value associated with a paired t-test. Here's how to utilize this function effectively.
- Organize Your Data: Ensure your data is arranged in a way that each row represents a pair of observations. For example, if you're comparing the pre- and post-test scores of a group of students, your data should be organized with pre-test scores in one column and post-test scores in another, with each row representing a student.
- Input the T.TEST Function: In an empty cell, enter the formula
=T.TEST(array1, array2, tails, type), wherearray1andarray2are the ranges containing the paired data,tailsrepresents the number of tails (1 for one-tailed, 2 for two-tailed), andtypespecifies the type of t-test (1 for paired samples, 2 for two-sample equal variance, and 3 for two-sample unequal variance). In our case, we'll usetypeas 1 for paired samples. - Interpret the Result: The T.TEST function returns the p-value associated with the paired t-test. This p-value can be directly compared to your chosen significance level to make statistical decisions. A p-value less than the significance level indicates a statistically significant difference between the paired observations.
Consider a study evaluating the effectiveness of a new teaching strategy on student performance. The data, representing pre- and post-test scores for a group of students, is as follows:
| Pre-Test | Post-Test |
|---|---|
| 85 | 92 |
| 78 | 85 |
| 90 | 95 |
| 82 | 88 |
| 80 | 84 |
Using the T.TEST function with the formula =T.TEST(B2:B6, C2:C6, 2, 1), we obtain a p-value of 0.0154. Since this p-value is less than the typical significance level of 0.05, we can conclude that the new teaching strategy has a statistically significant impact on student performance.
Method 3: Using Excel's Data Analysis ToolPak for Advanced Statistical Tests
For more complex statistical analyses, Excel's Data Analysis ToolPak offers a comprehensive suite of functions and tools. While this add-in is not enabled by default, it can be easily installed and activated, providing access to a wide range of statistical tests and calculations.
- Enable the Data Analysis ToolPak: If you haven't already, install and enable the Data Analysis ToolPak. Go to File > Options > Add-Ins, select Excel Add-ins, and click Go. Check the box next to Analysis ToolPak and click OK. The Data Analysis tool will now be available under the Data tab.
- Access the Data Analysis Tool: Under the Data tab, click on Data Analysis to open the Data Analysis dialog box. From here, you can select the appropriate statistical test, such as t-Test: Two-Sample Assuming Equal Variances, ANOVA: Single Factor, or Chi-Square Test, depending on your analysis needs.
- Input Data and Interpret Results: Follow the prompts to input your data and select the relevant options for your chosen statistical test. Once you've provided all the necessary information, click OK to perform the analysis. The results, including the p-value, will be displayed in a new worksheet, allowing you to make informed statistical decisions.
For instance, imagine you're conducting a study to compare the effectiveness of three different teaching methods. Your data, representing the test scores for each method, is as follows:
| Method A | Method B | Method C |
|---|---|---|
| 85 | 90 | 88 |
| 92 | 88 | 95 |
| 88 | 95 | 89 |
| 90 | 89 | 93 |
| 87 | 93 | 90 |
Using the Data Analysis ToolPak, you can perform a one-way ANOVA to determine if there are significant differences among the three teaching methods. The ANOVA results, including the p-value, will help you decide whether further post-hoc tests are necessary to identify specific differences between the methods.
💡 It's important to note that while Excel's built-in functions and the Data Analysis ToolPak offer convenient ways to calculate p-values, they may not always provide the most advanced or nuanced statistical analyses. For more complex research questions or when working with large datasets, specialized statistical software or programming languages might be more suitable.
Frequently Asked Questions
How accurate are p-values calculated in Excel compared to specialized software?
+Excel’s built-in functions and the Data Analysis ToolPak provide reasonably accurate p-values for most basic and intermediate statistical analyses. However, for highly complex or large-scale analyses, specialized software may offer more precise and advanced calculations.
Can I use Excel to calculate p-values for non-parametric tests like the Mann-Whitney U test or the Kruskal-Wallis H test?
+Excel does not have built-in functions for non-parametric tests. However, you can use the Data Analysis ToolPak to perform these tests, which will provide the necessary statistics, including the p-value.
What are the limitations of using Excel for p-value calculations in statistical analyses?
+Excel’s statistical functions may have limitations when dealing with complex datasets or advanced statistical models. Additionally, Excel may not always provide the most intuitive or user-friendly interface for advanced statistical analyses.



