4 Tips for Box Plot Boundary Calculations
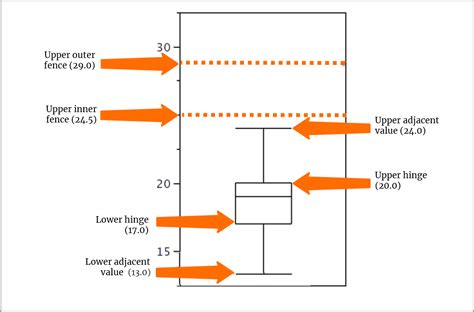
Box plots, also known as box-and-whisker plots, are an essential tool in data visualization and analysis. They provide a concise and informative way to understand the distribution of a dataset by displaying its quartiles and potential outliers. Accurate boundary calculations are crucial for constructing meaningful box plots, and in this article, we will delve into four expert tips to ensure precise and reliable calculations.
Understanding Box Plot Components

Before diving into the tips, let’s quickly review the key components of a box plot.
A box plot typically consists of the following elements:
- Median (Q2): The middle value of the dataset, dividing it into two halves.
- First Quartile (Q1): The median of the lower half of the dataset.
- Third Quartile (Q3): The median of the upper half of the dataset.
- Interquartile Range (IQR): The range between Q1 and Q3, representing the middle 50% of the data.
- Lower Whisker: Extends from Q1 to the lowest value within 1.5 * IQR of Q1.
- Upper Whisker: Extends from Q3 to the highest value within 1.5 * IQR of Q3.
- Potential Outliers: Points that fall outside the whisker range.
Tip 1: Sorting and Ordering Data

The foundation of accurate box plot boundary calculations lies in sorting and ordering the dataset.
Ensure that your data is arranged in ascending order. This step is critical because it allows for the correct identification of quartiles and outliers.
For example, consider the following dataset:
| Value |
|---|
| 2 |
| 8 |
| 12 |
| 14 |
| 18 |
| 20 |

When sorted, the dataset becomes:
| Value |
|---|
| 2 |
| 8 |
| 12 |
| 14 |
| 18 |
| 20 |
This ordering ensures that calculations for quartiles and boundaries are performed accurately.
Tip 2: Calculating Quartiles
Accurate quartile calculations are essential for determining the boundaries of the box plot.
The first quartile (Q1) is the median of the lower half of the dataset. To calculate it, follow these steps:
- Count the number of data points (n)
- Determine the position of Q1 using the formula: Q1 position = (n + 1) / 4
- If the position is a whole number, take the value at that position. If it’s not a whole number, interpolate between the two closest values.
For example, if n = 7, the Q1 position would be (7 + 1) / 4 = 2. Therefore, Q1 would be the value at position 2 in the sorted dataset.
Similarly, the third quartile (Q3) is the median of the upper half of the dataset. The formula for its position is: Q3 position = 3 * (n + 1) / 4
Tip 3: Determining Interquartile Range (IQR)
The interquartile range (IQR) is a measure of variability and is calculated as the difference between Q3 and Q1.
To find the IQR, subtract Q1 from Q3:
IQR = Q3 - Q1
The IQR provides a robust measure of variability, as it is less sensitive to outliers compared to the range.
Tip 4: Defining Whisker Boundaries

The whisker boundaries of a box plot are crucial for identifying potential outliers.
The lower whisker extends from Q1 to the lowest value within 1.5 * IQR of Q1. This range is calculated as follows:
Lower Whisker Boundary = Q1 - (1.5 * IQR)
Similarly, the upper whisker extends from Q3 to the highest value within 1.5 * IQR of Q3:
Upper Whisker Boundary = Q3 + (1.5 * IQR)
Values that fall outside these whisker boundaries are considered potential outliers and are represented as individual points in the box plot.
💡 It's important to note that these boundaries are based on the assumption that the dataset follows a symmetric distribution. In cases of skewed data, adjustments might be necessary to account for the asymmetry.
Practical Example
Let’s apply these tips to a practical example. Consider the following dataset:
| Value |
|---|
| 5 |
| 8 |
| 10 |
| 12 |
| 15 |
| 18 |
| 20 |
Step 1: Sorting and Ordering
Sort the dataset in ascending order:
| Value |
|---|
| 5 |
| 8 |
| 10 |
| 12 |
| 15 |
| 18 |
| 20 |
Step 2: Calculating Quartiles
With n = 7, we can calculate the positions of Q1 and Q3:
- Q1 position = (7 + 1) / 4 = 2
- Q3 position = 3 * (7 + 1) / 4 = 5.25
Interpolating between the two closest values for Q3, we get:
Q1 = 8, Q2 (Median) = 12, Q3 = 15
Step 3: Determining IQR
Calculate the IQR:
IQR = Q3 - Q1 = 15 - 8 = 7
Step 4: Defining Whisker Boundaries
Find the whisker boundaries:
- Lower Whisker Boundary = Q1 - (1.5 * IQR) = 8 - (1.5 * 7) = 8 - 10.5 = -2.5
- Upper Whisker Boundary = Q3 + (1.5 * IQR) = 15 + (1.5 * 7) = 15 + 10.5 = 25.5
Box Plot Visualization
With the calculated boundaries, we can now visualize the box plot.
The box plot for this dataset would look like this:
| Value | Lower Whisker | Box | Upper Whisker | |
|---|---|---|---|---|
| 5 | -2.5 | 8 | 15 | 25.5 |
Conclusion
Accurate box plot boundary calculations are fundamental for effectively visualizing and analyzing data distributions. By following the tips outlined in this article, you can ensure precise and reliable box plots.
Remember, sorting and ordering your data, calculating quartiles, determining the IQR, and defining whisker boundaries are crucial steps to create meaningful box plots. With these techniques, you’ll be able to uncover valuable insights and better understand the characteristics of your dataset.
What are the benefits of using box plots for data visualization?
+Box plots offer a concise and effective way to visualize data distributions, highlighting key statistics such as quartiles, median, and potential outliers. They provide a quick overview of the dataset’s spread and variability, making them a valuable tool for data analysis and comparison.
How do I handle datasets with a large number of outliers?
+When dealing with datasets that have a high number of outliers, you might need to adjust your whisker boundaries. Instead of using 1.5 * IQR, consider using a more conservative value like 2 * IQR to capture a larger portion of the data within the whiskers. This approach can help ensure that the box plot provides a more representative view of the dataset’s distribution.
Can box plots be used for non-numerical data?
+While box plots are primarily designed for numerical data, there are adaptations for categorical or ordinal data. In these cases, each category or level of the variable is represented by a separate box plot, allowing for comparisons between different groups.



