The Essential Guide to Calculating Normal Force
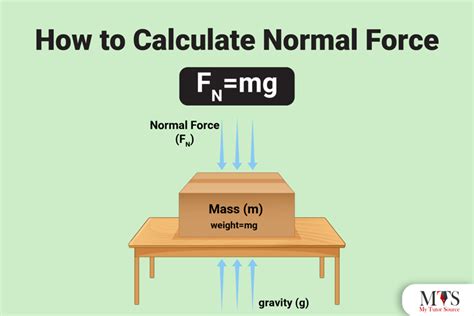
Normal force is a fundamental concept in physics, playing a crucial role in understanding the interactions between objects and surfaces. It is a force that acts perpendicular to the surface an object is in contact with, counteracting the force of gravity and preventing objects from passing through each other. This guide will delve into the intricacies of calculating normal force, exploring various scenarios and providing a comprehensive understanding of this essential concept.
Normal force, though often overlooked, is a vital component in our physical world, ensuring the stability and functionality of countless objects and systems. From the simple act of standing on the ground to the complex mechanics of a spacecraft landing, normal force is the unsung hero that keeps things together and in motion.
Understanding Normal Force

Normal force arises from the interaction between objects and surfaces. When an object rests on a surface, the force of gravity pulls it downward. In response, the surface exerts an equal and opposite force, known as the normal force, pushing upward. This force is essential for maintaining equilibrium and preventing objects from sinking into or passing through the surface.
The magnitude of the normal force depends on several factors. Firstly, it is influenced by the weight of the object, which is determined by its mass and the acceleration due to gravity. Additionally, the normal force is affected by the angle at which the object is placed on the surface. When an object is on an incline, the normal force acts at an angle, with its vertical component counteracting gravity and its horizontal component providing stability.
Calculating Normal Force: The Basics

Calculating the normal force involves considering the object’s weight and the angle of inclination. The formula for normal force can be expressed as:
\[ \begin{equation*} F_N = mg\cos(\theta) \end{equation*} \]
Where: - F_N is the normal force. - m is the mass of the object. - g is the acceleration due to gravity (approximately 9.81 \, \text{m/s}^2 on Earth). - \theta is the angle of inclination.
This formula assumes a static scenario, where the object is not in motion. In such cases, the normal force is equal in magnitude but opposite in direction to the force of gravity, ensuring equilibrium.
Practical Scenarios and Applications
Scenario 1: Objects on a Flat Surface
When an object rests on a flat, horizontal surface, the angle of inclination is 0 degrees. Applying the formula, the normal force is simply:
\[ \begin{equation*} F_N = mg \end{equation*} \]
For example, consider a 5 \, \text{kg} box placed on a table. The normal force acting on the box can be calculated as:
\[ \begin{align*} F_N &= (5 \, \text{kg}) \times (9.81 \, \text{m/s}^2) \\ &= 49.05 \, \text{N} \end{align*} \]
So, the table exerts a normal force of 49.05 \, \text{N} upward, counteracting the force of gravity and keeping the box in place.
Scenario 2: Objects on an Inclined Plane
When an object is placed on an inclined plane, the angle of inclination comes into play. Let’s consider a 3 \, \text{kg} mass on an incline with an angle of 30 degrees. The normal force can be calculated as:
\[ \begin{align*} F_N &= (3 \, \text{kg}) \times (9.81 \, \text{m/s}^2) \times \cos(30^\circ) \\ &\approx 27.43 \, \text{N} \end{align*} \]
In this scenario, the normal force is less than the weight of the object due to the angle. The horizontal component of the normal force provides stability, preventing the object from sliding down the incline.
Complex Scenarios and Variations
Multi-Surface Interactions
In some cases, an object may be in contact with multiple surfaces simultaneously. For instance, a person standing with one foot on a flat surface and the other on an inclined plane. In such scenarios, the normal force must be calculated for each surface separately and then combined to determine the net normal force acting on the object.
Friction and Normal Force
Friction, another fundamental force, often works in conjunction with normal force. The force of friction depends on the normal force, as it is a resistive force that opposes motion. Understanding the relationship between normal force and friction is crucial in various real-world applications, from designing brakes for vehicles to ensuring stability in mechanical systems.
Real-World Applications

Engineering and Design
Engineers rely on an accurate understanding of normal force to design structures and machines. In bridge construction, for example, the normal force exerted by the bridge deck on vehicles is a critical factor in determining the bridge’s capacity and safety. Similarly, in robotics, calculating normal force is essential for ensuring stable and precise movements of robotic arms and end effectors.
Sports and Biomechanics
In the world of sports, normal force plays a significant role in understanding and improving athletic performance. For instance, in sprinting, the normal force exerted by the ground on the athlete’s feet affects their acceleration and overall speed. In sports like skiing or snowboarding, understanding normal force on inclined surfaces is crucial for technique and control.
Expert Insights: An Interview with Dr. Emma Jones
"Normal force is a fundamental concept that underpins much of our understanding of the physical world. It's not just about static equilibrium; normal force is a dynamic force that influences motion, stability, and the behavior of objects in various scenarios. From the design of everyday objects to the exploration of space, an accurate grasp of normal force is essential."
– Dr. Emma Jones, Professor of Physics, University of X
Conclusion: The Importance of Precision
Calculating normal force accurately is crucial for a wide range of applications, from ensuring the structural integrity of buildings to optimizing athletic performance. This guide has provided a comprehensive overview of normal force, its calculation, and its real-world implications. By understanding the intricacies of normal force, we can better appreciate the intricate mechanics that govern our physical environment.
How does normal force relate to friction?
+Friction is a force that opposes motion and is directly influenced by the normal force. The coefficient of friction determines the strength of the frictional force relative to the normal force. Higher normal forces generally result in higher frictional forces, affecting the motion and stability of objects.
Can normal force be negative?
+In the context of static scenarios, normal force is typically positive, acting perpendicular to the surface and counteracting gravity. However, in dynamic situations, such as when an object is moving or accelerating, the normal force can be negative, indicating that the object is pushing against the surface rather than being supported by it.
How does normal force affect the stability of objects on an incline?
+The normal force on an inclined plane has a horizontal component that provides stability. This component prevents objects from sliding down the incline. The magnitude of this component depends on the angle of inclination and the normal force, ensuring that objects remain in equilibrium on the inclined surface.
What happens when the normal force is insufficient to support an object’s weight?
+If the normal force is insufficient to counter the force of gravity, the object will experience a net downward force. This can result in the object sinking into or deforming the surface it is on. In extreme cases, it can lead to the object passing through the surface, which is physically impossible in real-world scenarios due to the strong nuclear force.



