Mastering Asymptotes: 3 Essential Techniques

Asymptotes are a fundamental concept in mathematics, especially in calculus and graphing functions. These mathematical constructs can be a source of confusion for many students, but with the right techniques, understanding and mastering asymptotes becomes an achievable goal. In this comprehensive guide, we will explore three essential techniques that will empower you to tackle asymptotes with confidence and precision.
Understanding the Nature of Asymptotes
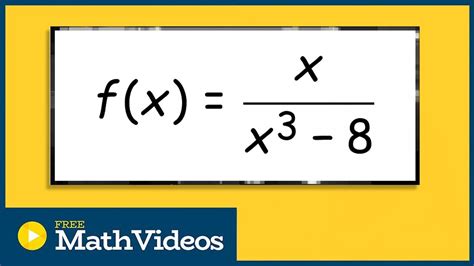
Before we delve into the techniques, it’s crucial to grasp the essence of asymptotes. In mathematics, an asymptote is a line or curve that a function approaches as the input (usually denoted as x) tends towards a certain value. There are three main types of asymptotes:
Vertical Asymptotes: These are vertical lines that the function approaches as x gets closer to a specific value, often representing a point of discontinuity.
Horizontal Asymptotes: Unlike vertical asymptotes, horizontal asymptotes are horizontal lines that the function approaches as x tends towards positive or negative infinity.
Oblique or Slant Asymptotes: This type of asymptote is a diagonal line that the function approaches as x becomes extremely large (positive or negative).
Technique 1: Analyzing the Function’s Behavior

The first step in mastering asymptotes is to analyze the behavior of the function at critical points. These critical points are where the function may exhibit interesting or unusual behavior, such as approaching an asymptote. To identify these points, you can employ the following strategies:
- Locate the Vertical Asymptotes: Look for values of x where the denominator of the function becomes zero. These values indicate potential vertical asymptotes.
For example, in the function $f(x) = \frac{1}{(x - 2)(x + 3)}$, the vertical asymptotes occur at $x = 2$ and $x = -3$ because these are the values that make the denominator zero.
- Determine the Horizontal Asymptotes: Examine the behavior of the function as x tends towards positive and negative infinity. If the function approaches a constant value in either direction, that value represents a horizontal asymptote.
Consider the function $g(x) = \frac{2x + 5}{x^2 + 3x + 2}$. As $x$ approaches positive infinity, the function approaches the horizontal asymptote $y = 2$, while as $x$ approaches negative infinity, the function approaches the same asymptote.
- Identify Oblique Asymptotes: For rational functions (functions that can be expressed as the ratio of two polynomials), the oblique asymptote can be found by dividing the numerator polynomial by the denominator polynomial. The remainder of this division gives the equation of the oblique asymptote.
In the function $h(x) = \frac{3x^2 + 5x + 2}{x - 1}$, dividing the numerator by the denominator yields the equation of the oblique asymptote: $y = 3x + 8$.
Technique 2: Using Limits to Confirm Asymptotes
Limits provide a powerful tool to confirm the existence and nature of asymptotes. By calculating limits, you can rigorously determine whether a function indeed approaches a specific line or curve as x tends towards a certain value. Here’s how you can utilize limits:
- Vertical Asymptotes: Calculate the limit of the function as x approaches the suspected vertical asymptote from both sides (left and right). If the limit exists and is different for each side, then a vertical asymptote is confirmed.
For the function $f(x) = \frac{1}{x - 2}$, we find that $\lim_{x \to 2^-} f(x) = -\infty$ and $\lim_{x \to 2^+} f(x) = \infty$. This confirms the vertical asymptote at $x = 2$.
- Horizontal Asymptotes: Calculate the limit of the function as x approaches positive and negative infinity. If the limit exists and is a constant value, then a horizontal asymptote is confirmed.
For the function $g(x) = \frac{2x + 5}{x^2 + 3x + 2}$, we find that $\lim_{x \to \infty} g(x) = 2$ and $\lim_{x \to -\infty} g(x) = 2$. This confirms the horizontal asymptote $y = 2$.
- Oblique Asymptotes: Calculate the limit of the function as x approaches infinity. If the limit exists and is a linear function, then an oblique asymptote is confirmed.
For the function $h(x) = \frac{3x^2 + 5x + 2}{x - 1}$, we find that $\lim_{x \to \infty} h(x) = 3x + 8$. This confirms the oblique asymptote $y = 3x + 8$.
Technique 3: Graphical Interpretation and Visualization
Visualizing the behavior of functions and their asymptotes is a powerful technique for gaining intuitive understanding. Graphical representation allows you to see how the function approaches the asymptotes and how they relate to each other. Here’s how you can use graphical tools:
- Plot the Function: Create a graph of the function over a wide range of x-values, including the suspected asymptotes.
Plotting the function $f(x) = \frac{1}{x - 2}$ reveals that as $x$ gets closer to 2 from both sides, the function approaches the vertical asymptote.
Highlight Asymptotes: On the same graph, draw the asymptotes as dashed lines. This helps to visually identify how the function behaves near these lines.
Analyze Curvature: Observe the curvature of the function near the asymptotes. Vertical asymptotes often result in a sharp turn or infinite slope, while horizontal asymptotes show a flattening of the curve as x approaches infinity.
In the function $g(x) = \frac{2x + 5}{x^2 + 3x + 2}$, the horizontal asymptote $y = 2$ is clearly visible as the curve flattens out as $x$ becomes extremely large.
Key Takeaways

Asymptotes are essential mathematical concepts that represent the behavior of functions as they approach certain values of x.
There are three main types of asymptotes: vertical, horizontal, and oblique.
Analyzing the function’s behavior, using limits to confirm asymptotes, and employing graphical interpretation are three powerful techniques for mastering asymptotes.
Understanding asymptotes not only enhances your mathematical skills but also has practical applications in fields like engineering, physics, and computer science.
Further Exploration
Asymptotes are just the beginning of exploring the fascinating world of calculus and mathematical analysis. To continue your journey, consider delving into these related topics:
Infinite Series: Explore the concept of infinite series and how they relate to asymptotic behavior.
Differential Equations: Understand how asymptotes can be used to solve differential equations and model real-world phenomena.
L’Hôpital’s Rule: Learn this powerful rule for evaluating limits, especially when dealing with indeterminate forms.
Remember, mathematics is a journey of discovery, and asymptotes are just one fascinating aspect of this vast and beautiful field. With practice and a deep understanding of these techniques, you’ll be well on your way to mastering asymptotes and unlocking new mathematical insights.
How do I know if a function has a vertical asymptote at a specific point?
+To determine if a function has a vertical asymptote at a specific point, check if the denominator of the function becomes zero at that point. If the denominator is zero and the numerator is not, then a vertical asymptote exists at that point.
<div class="faq-item">
<div class="faq-question">
<h3>Can a function have multiple horizontal asymptotes?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>No, a function cannot have multiple horizontal asymptotes. Horizontal asymptotes represent the long-term behavior of the function as $x$ tends towards infinity or negative infinity. A function can only approach one constant value in either direction.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What happens if a function has no horizontal or oblique asymptotes?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>If a function has no horizontal or oblique asymptotes, it means that as $x$ approaches positive or negative infinity, the function does not approach any constant value. In such cases, the function may oscillate, grow unbounded, or exhibit other unique behaviors.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How can I visually identify oblique asymptotes on a graph?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Oblique asymptotes can be visually identified on a graph by looking for a line that the function approaches as $x$ becomes extremely large. The function's curve will gradually align with this line, indicating the presence of an oblique asymptote.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Are there any functions that don't have any asymptotes at all?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Yes, there are functions that don't have any asymptotes. For example, a simple quadratic function like $f(x) = ax^2 + bx + c$ will not have any asymptotes as long as the coefficients $a$, $b$, and $c$ are real numbers and $a$ is not zero.</p>
</div>
</div>
</div>