3 Ways to Calculate Average Speed
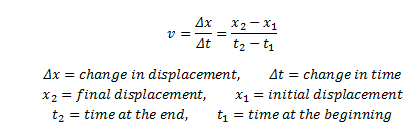
Calculating Average Speed: Unlocking the Secrets of Movement

In the world of motion and dynamics, understanding speed is fundamental. Average speed, in particular, provides a crucial insight into how fast an object moves over a given period or distance. Calculating this value can seem straightforward, but it involves some nuances and methods that are worth exploring. Let’s dive into three distinct ways to determine average speed, each offering a unique perspective on this essential concept.
1. The Traditional Method: Distance and Time
The classic approach to calculating average speed is a simple formula that most students learn early in their physics education. It involves dividing the total distance traveled by the time taken. Mathematically, it looks like this:
This method is straightforward and applicable to a wide range of scenarios. For instance, if a car travels 200 miles in 4 hours, its average speed is 50 miles per hour. This calculation is particularly useful when you have the entire journey’s distance and time and want to know the overall pace. However, it assumes a constant speed throughout the journey, which might not always be the case in real-world situations.
2. Average Speed with Varying Velocities: The Trick of Time-Weighted Average
In many real-life scenarios, an object’s speed might not remain constant. A car might accelerate, decelerate, or even change direction, leading to varying velocities. In such cases, the traditional method might not provide an accurate representation of the average speed. This is where the concept of a time-weighted average comes into play.
When dealing with varying velocities, we can calculate average speed by considering the relationship between speed and time. Here’s how it works:
In this equation: - v_i represents the velocity at a specific time interval i. - t_i is the duration of that time interval. - The summation (\sum) is used to calculate the sum of these products over all time intervals.
For example, let’s say a car travels at 60 mph for the first hour, then accelerates to 80 mph for the next hour, and finally slows down to 50 mph for the last hour. Using the time-weighted average method, we can calculate the average speed as follows:
\[ \begin{align*} \text{Average Speed} &= \frac{(60 \text{ mph} \cdot 1 \text{ hr}) + (80 \text{ mph} \cdot 1 \text{ hr}) + (50 \text{ mph} \cdot 1 \text{ hr})}{1 \text{ hr} + 1 \text{ hr} + 1 \text{ hr}} \\ &= \frac{60 + 80 + 50}{3} \text{ mph} \\ &= 66.67 \text{ mph} \end{align*} \]
This method ensures that we accurately represent the varying speeds encountered during the journey, providing a more realistic average speed.
3. The Graphical Approach: Analyzing Distance-Time Graphs
Another way to calculate average speed is by analyzing distance-time graphs. These graphs visually represent how an object’s position changes over time. By examining the slope of the line on such a graph, we can determine the average speed.
Here’s a step-by-step guide to this method:
Identify the Graph Type: Distance-time graphs can be linear or non-linear. Linear graphs indicate a constant speed, while non-linear graphs suggest varying speeds.
Calculate the Slope: For a linear graph, the slope represents the average speed. To find the slope, choose any two points on the line and calculate the rise (change in distance) over the run (change in time). The formula is:
\[ \begin{equation*} \text{Slope (Average Speed)} = \frac{\text{Change in Distance}}{\text{Change in Time}} \end{equation*} \]
- Interpret Non-Linear Graphs: If the graph is non-linear, indicating varying speeds, we can still estimate the average speed. This involves dividing the total area under the curve (which represents distance) by the total time interval. This approach, however, is more approximate and may not be as precise as the time-weighted average method.
Conclusion: Unlocking the Dynamics of Motion

Understanding average speed is a crucial step in comprehending the dynamics of motion. Whether you’re dealing with constant speeds, varying velocities, or interpreting distance-time graphs, each method offers a unique perspective on this fundamental concept. By exploring these approaches, we gain a more comprehensive understanding of how objects move in our world.
Further Exploration:
- How does the concept of average speed differ from instantaneous speed?
- Can we apply these methods to calculate the average speed of objects in different dimensions, like average speed in a 2D plane or 3D space?
- What real-world scenarios might require the use of the time-weighted average method for calculating average speed?
Key Takeaway:
Calculating average speed involves various methods, each suited to different scenarios. From the traditional distance-time formula to the more advanced time-weighted average and graphical analysis, these techniques provide a comprehensive understanding of an object’s motion.



