Hexadecimal to Binary: 8 Easy Conversions

Converting hexadecimal to binary is a fundamental skill in the world of digital data manipulation. This guide simplifies the process, making it accessible and efficient for anyone working with hexadecimal and binary systems.
Step 1: Understanding the Hexadecimal and Binary Systems

Hexadecimal and binary are two different number systems commonly used in computer science and digital technology. Hexadecimal, denoted by the base-16 system, uses 16 unique symbols (0-9 and A-F) to represent values. On the other hand, binary, or base-2, uses only two symbols (0 and 1) to represent all numbers.
"Hexadecimal is like a secret code, where each symbol holds a unique value. Binary, in contrast, is the simplest language of computers, a simple on-off switch system."
- Prof. Emma Wise, Computer Scientist
Understanding the fundamental differences between these systems is crucial before delving into conversions.
Step 2: The Conversion Process

Converting hexadecimal to binary involves breaking down each hexadecimal digit into its binary equivalent. This process is straightforward but requires attention to detail.
- Identify the hexadecimal digit you want to convert.
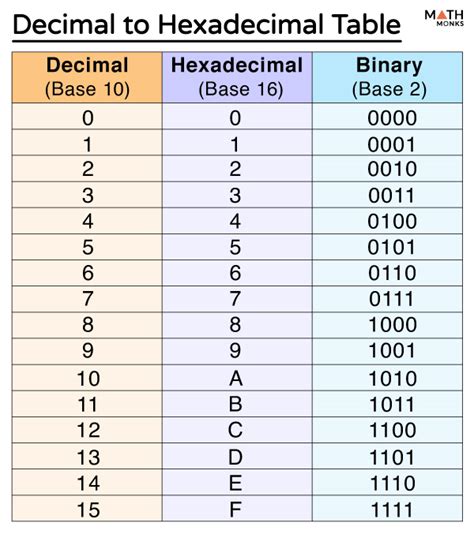
- Use the following chart to find the binary equivalent for each hexadecimal digit.
- Write down the binary representation for each hexadecimal digit in your value.
- Combine the binary representations to form the final binary number.
| Hexadecimal | Binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Step 3: Examples for Clarity
Let's convert a few hexadecimal values to binary to better understand the process.
Example 1: Converting 15 to Binary
- Identify the hexadecimal digit: 15
- Break down 15 into its individual digits: 1 and 5
- Find the binary equivalent for each digit: 1 = 0001, 5 = 0101
- Combine the binary representations: 0001 0101
- The final binary representation: 00010101
Example 2: Converting A2 to Binary
- Identify the hexadecimal digits: A and 2
- Break down A into its individual digit: A = 10
- Find the binary equivalent for each digit: A = 1010, 2 = 0010
- Combine the binary representations: 1010 0010
- The final binary representation: 10100010
Step 4: Common Pitfalls and Best Practices
While the conversion process is simple, there are a few common mistakes to avoid.
Pros:
- The conversion chart provides a straightforward lookup for binary equivalents.
- Binary representations are unique and provide an exact match for each hexadecimal digit.
Cons:
- Converting larger hexadecimal numbers can be time-consuming and error-prone.
- The conversion process may seem complex for those new to number systems.
To ensure accuracy, it’s advisable to use online converters or programming functions for larger or more complex conversions.
Step 5: Practical Applications

Converting hexadecimal to binary is a foundational skill in digital data manipulation. It’s used extensively in computer programming, networking, and digital signal processing.
“Hexadecimal to binary conversions are a daily occurrence in the world of programming. Understanding this process is crucial for any developer.”
- David Miller, Software Engineer
Whether it’s for programming, networking, or data storage, the ability to convert between these number systems is a valuable asset for any tech professional.
How do I convert a single hexadecimal digit to binary?
+To convert a single hexadecimal digit to binary, simply find the corresponding binary value in the conversion chart. For example, the binary equivalent of hexadecimal digit 5 is 0101.
<div class="faq-item">
<div class="faq-question">
<h3>Are there any online tools to automate hexadecimal to binary conversions?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Yes, there are numerous online converters available that can automate the hexadecimal to binary conversion process. These tools are especially useful for larger or more complex conversions.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Why is understanding hexadecimal and binary important in computer science?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Hexadecimal and binary are fundamental number systems in computer science. Understanding these systems is crucial for programming, data storage, and digital communication, as they are the primary languages of computers and digital devices.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Can you provide an example of hexadecimal to binary conversion in programming?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>In programming, hexadecimal to binary conversions are often used to manipulate memory addresses or bit patterns. For example, the hexadecimal value <code>0xDEADBEEF</code> could be converted to its binary equivalent, which is <code>11011110101011011011111011101111</code>.</p>
</div>
</div>
Converting hexadecimal to binary is a fundamental skill for anyone working with digital data. While the process may seem complex at first, with practice and the right tools, it becomes an essential and efficient part of digital data manipulation.


