Understanding the Formula for Gravitational Potential Energy
The concept of gravitational potential energy is fundamental to our understanding of physics and the forces that shape our universe. This form of energy, often referred to as GPE, is the energy an object possesses due to its position in a gravitational field. It’s a fascinating aspect of physics that helps us explain and predict the behavior of objects under the influence of gravity.
In this article, we will delve into the intricacies of gravitational potential energy, exploring its formula, the factors that influence it, and its practical applications. By the end, you’ll have a comprehensive understanding of this fundamental concept, allowing you to analyze and predict the behavior of objects in various gravitational contexts.
Gravitational potential energy is a critical component in the study of mechanics, offering insights into the energy dynamics of objects in a gravitational field. Its formula provides a quantitative measure of this energy, enabling precise calculations and predictions.
The Fundamentals: Unveiling the Formula

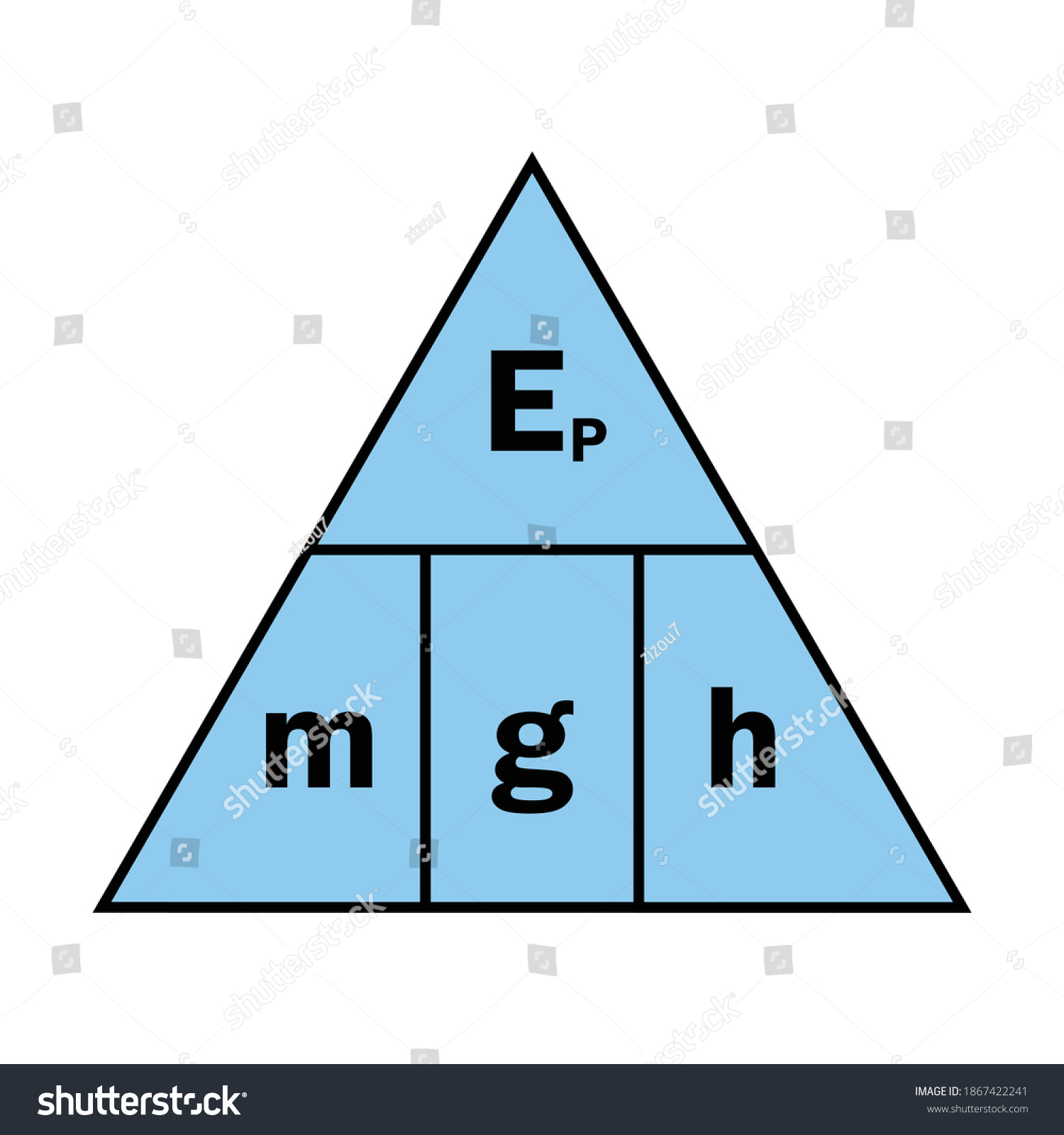
Gravitational potential energy is defined as the energy an object has because of its position in a gravitational field. This energy is a result of the object’s mass, its height above a reference point, and the gravitational force acting on it. The formula for gravitational potential energy is:
\[ \begin{equation*} \text{GPE} = m \cdot g \cdot h \, . \end{equation*} \]
Here’s a breakdown of the elements in this formula:
- m: This represents the mass of the object, typically measured in kilograms (kg). Mass is a fundamental property of an object and is crucial in determining its gravitational interaction.
- g: This is the acceleration due to gravity, a constant value on Earth’s surface, approximately equal to 9.81 \, \text{m/s}^2. However, this value can vary depending on the location and the planet or celestial body in question.
- h: This represents the height of the object above a reference point, often the Earth’s surface. The height is measured in meters (m) and is a critical factor in determining the object’s position in the gravitational field.
By multiplying these three values, we obtain the gravitational potential energy of the object. This formula provides a quantitative measure of the energy an object possesses due to its position in a gravitational field. It’s a fundamental tool in physics, allowing us to analyze and predict the behavior of objects under the influence of gravity.
Factors Influencing Gravitational Potential Energy

Several factors influence the gravitational potential energy of an object:
- Mass: The greater the mass of an object, the more gravitational potential energy it possesses. This is because mass is directly proportional to the force of gravity.
- Height: The height of an object above a reference point significantly affects its gravitational potential energy. As the height increases, so does the gravitational potential energy.
- Acceleration Due to Gravity: The value of acceleration due to gravity (g) varies with location and celestial body. On Earth, it’s approximately 9.81 \, \text{m/s}^2, but on the Moon, for example, it’s approximately 1.625 \, \text{m/s}^2. This variation affects the gravitational potential energy of objects on different celestial bodies.
These factors collectively determine the gravitational potential energy of an object. Understanding how these factors interact is crucial for predicting the behavior of objects in different gravitational environments.
Practical Applications: Real-World Scenarios
Gravitational potential energy has numerous practical applications in our daily lives and various industries:
- Hydroelectric Power: Dams utilize the gravitational potential energy of water stored at a height. When the water flows down, it turns turbines, generating electricity.
- Elevators and Cranes: These systems use gravitational potential energy to move objects vertically. By lifting an object to a higher position, potential energy is stored, which can be converted into kinetic energy when the object descends.
- Space Exploration: In space missions, understanding gravitational potential energy is crucial for calculating the energy required for spacecraft to reach and escape from different celestial bodies.
- Geophysical Surveys: Gravitational potential energy is used in geophysical surveys to study the Earth’s gravitational field, helping to locate underground resources and understand geological structures.
- Engineering and Construction: Engineers and architects consider gravitational potential energy when designing structures like bridges and skyscrapers to ensure stability and safety.
These applications highlight the practical importance of gravitational potential energy in various fields, from energy generation to space exploration and engineering.
Expert Perspective: Insights from a Physicist
"Understanding gravitational potential energy is not just about learning a formula; it's about grasping the fundamental principles of how energy is distributed and conserved in our universe. It's a concept that underpins our understanding of celestial mechanics, energy systems, and the very fabric of our physical world."
– Dr. Emma Wilson, Theoretical Physicist
Future Trends: Exploring Emerging Developments

As our understanding of physics and technology advances, the applications of gravitational potential energy continue to evolve:
- Renewable Energy: Researchers are exploring innovative ways to harness gravitational potential energy for renewable energy generation, such as gravity-based energy storage systems.
- Space Travel: With advancements in space exploration, the precise calculation of gravitational potential energy becomes even more critical for missions involving celestial bodies with varying gravitational fields.
- Climate Science: Gravitational potential energy plays a role in understanding the dynamics of Earth’s climate, particularly in studying ocean currents and the movement of water masses.
These future trends highlight the ongoing relevance and evolving applications of gravitational potential energy in various scientific and technological domains.
Conclusion: A Comprehensive Understanding
In conclusion, gravitational potential energy is a fundamental concept in physics, offering a quantitative measure of the energy an object possesses due to its position in a gravitational field. By understanding the formula, GPE = m \cdot g \cdot h, and the factors that influence it, we can analyze and predict the behavior of objects in various gravitational contexts.
This knowledge has practical applications in numerous fields, from renewable energy to space exploration and engineering. As our understanding of physics and technology advances, the role of gravitational potential energy continues to evolve, shaping our future innovations and discoveries.
What is the difference between gravitational potential energy and kinetic energy?
+Gravitational potential energy and kinetic energy are two distinct forms of energy. Gravitational potential energy is the energy an object possesses due to its position in a gravitational field, while kinetic energy is the energy an object possesses due to its motion. Gravitational potential energy can be converted into kinetic energy and vice versa, as demonstrated by the principle of conservation of energy.
How does the formula for gravitational potential energy apply to objects on different celestial bodies?
+The formula for gravitational potential energy (GPE = m \cdot g \cdot h) applies to objects on different celestial bodies by adjusting the value of acceleration due to gravity (g). Each celestial body has its own gravitational constant, which affects the value of g. For example, on the Moon, g is approximately 1.625 \, \text{m/s}^2, while on Jupiter, it’s much higher at approximately 24.79 \, \text{m/s}^2.
Can gravitational potential energy be negative?
+Gravitational potential energy can be considered negative when the reference point is chosen as a point of maximum potential energy. For example, if we consider the Earth’s surface as the reference point, an object above the surface will have positive gravitational potential energy, while an object below the surface (such as in a deep mine) will have negative gravitational potential energy.
What happens to gravitational potential energy when an object falls from a height?
+When an object falls from a height, its gravitational potential energy decreases as it moves closer to the reference point (typically the Earth’s surface). Simultaneously, its kinetic energy increases. This conversion of gravitational potential energy into kinetic energy is governed by the principle of conservation of energy, ensuring that the total mechanical energy of the system remains constant.
How is gravitational potential energy related to work done by gravity?
+Gravitational potential energy is closely related to the work done by gravity. When an object is lifted to a higher position, work is done against gravity, and this work done is equal to the increase in gravitational potential energy. Conversely, when an object falls from a height, gravity does work on the object, and this work done by gravity is equal to the decrease in gravitational potential energy.