Understanding the lnx Graph: 3 Key Insights

The Domain and Range: An Exclusive Club

One of the first intriguing characteristics of the ln(x) graph is its domain and range. Unlike many other functions, the natural logarithm function has a very specific set of rules for what values of x it can accept and what values it can produce.
The domain of ln(x) is restricted to positive real numbers only. This means that the function simply doesn’t exist for negative or zero values of x. It’s like an exclusive club where only positive numbers are allowed entry.
As for the range, the ln(x) graph produces all real numbers, both positive and negative. This means that as x increases from 1, the value of ln(x) also increases positively, but as x decreases from 1 towards zero, the value of ln(x) decreases, becoming more and more negative.
This unique characteristic of the ln(x) graph, where the range spans the entire real number line, makes it a powerful tool for various mathematical and scientific applications.
Asymptotic Behavior: The Dance of the Curve
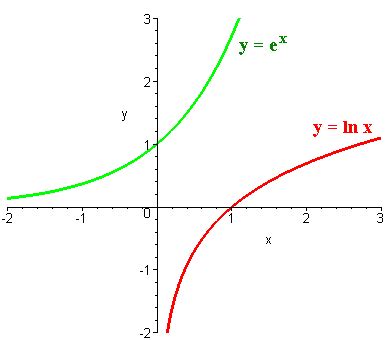
The ln(x) graph exhibits a captivating behavior known as asymptotic behavior. Asymptotes are lines that a curve approaches but never touches. In the case of ln(x), there are two key asymptotes: the x-axis and the vertical line at x = 1.
As x approaches zero from the right, the curve of ln(x) drops rapidly towards negative infinity, but it never actually touches the x-axis. Similarly, as x approaches 1 from either side, the curve flattens out and gets infinitely close to the vertical line at x = 1, but again, it never touches it.
This asymptotic behavior gives the ln(x) graph a unique shape and makes it particularly useful for modeling certain physical phenomena, especially in fields like physics and engineering.
The Vertical Line Test: A Curve’s Identity
Another fascinating aspect of the ln(x) graph is its unique behavior with respect to the vertical line test. This test is a fundamental concept in mathematics, used to determine if a curve represents a function or not.
The vertical line test states that if a vertical line intersects a curve in more than one point, then the curve does not represent a function. In the case of ln(x), the vertical line test is passed with flying colors.
No matter how you draw a vertical line on the ln(x) graph, it will only intersect the curve at a single point. This is because for any given value of x, there is only one corresponding value of y (the logarithm of that x). This property ensures that the ln(x) graph is indeed a true function, making it a reliable and consistent mathematical tool.
How does the ln(x) graph differ from other logarithmic graphs?
+The ln(x) graph differs from other logarithmic graphs primarily due to its base. While other logarithmic functions, such as log10(x) or log2(x), have specific bases (base 10 and base 2 respectively), the natural logarithm function has a base of e, a unique mathematical constant approximately equal to 2.71828. This choice of base gives the ln(x) graph its distinctive properties, such as its exclusive domain and range.
<div class="faq-item">
<div class="faq-question">
<h3>What are some real-world applications of the ln(x) function and its graph?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>The ln(x) function and its graph find applications in various fields. In physics, it's used to model the decay of radioactive substances and the cooling of objects. In engineering, it's applied in circuit analysis and control systems. In economics, it's used in models of inflation and growth. Even in biology, it's employed to describe the growth of certain populations.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Can the ln(x) graph be transformed or manipulated like other functions?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Absolutely! Just like any other function, the ln(x) graph can be transformed through various operations. You can shift it vertically or horizontally, stretch or compress it, reflect it across axes, and even combine it with other functions. These transformations allow for a wide range of applications and problem-solving scenarios.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Are there any notable historical figures associated with the development of the ln(x) function and its graph?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>The development of the natural logarithm function is closely tied to the work of John Napier, a Scottish mathematician who introduced logarithms in the early 17th century. However, it was Leonhard Euler, a Swiss mathematician, who popularized the use of the base e and its associated natural logarithm function in the 18th century.</p>
</div>
</div>
</div>



