Uncover the GCF of 32 and 24
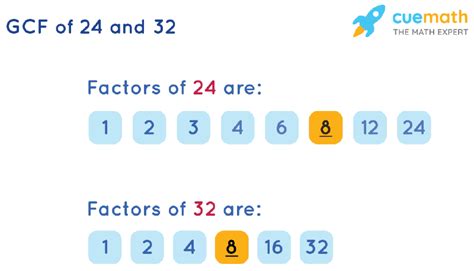
In mathematics, the greatest common factor (GCF) or greatest common divisor (GCD) of two or more integers is the largest positive integer that evenly divides the numbers without leaving a remainder. The GCF is a fundamental concept in number theory and has numerous practical applications in various fields, including computer science, engineering, and cryptography. In this article, we will delve into the process of finding the GCF of 32 and 24, exploring the methods and insights that mathematicians and computer scientists employ to tackle such problems.
Prime Factorization Method

One of the most intuitive and widely used methods to determine the GCF is through prime factorization. Prime factorization involves expressing a number as a product of prime factors. By finding the prime factors of 32 and 24, we can identify the common factors that contribute to the GCF.
Let’s start by finding the prime factors of each number:
- Prime factors of 32: 2 x 2 x 2 x 2 x 2
- Prime factors of 24: 2 x 2 x 2 x 3
Now, to find the GCF, we identify the common prime factors and multiply them, ensuring that we only consider the factors with the lowest exponent.
In this case, the common prime factors are 2 x 2 x 2, as both numbers have three occurrences of the prime factor 2. Thus, the GCF of 32 and 24 is 2 x 2 x 2, which equals 8.
Euclidean Algorithm

The Euclidean algorithm is another powerful method for calculating the GCF of two numbers. This algorithm, named after the ancient Greek mathematician Euclid, is based on the principle that the GCF of two numbers remains the same when one of the numbers is replaced by their difference.
To apply the Euclidean algorithm to find the GCF of 32 and 24, we perform the following steps:
- Subtract the smaller number (24) from the larger number (32) to get 8.
- Repeat the process by subtracting the smaller number (8) from the larger number (24) until we reach a remainder of 0.
In this case, the sequence of calculations is as follows:
- 32 - 24 = 8
- 24 - 8 = 16
- 16 - 8 = 8
- 8 - 8 = 0
Since we reach a remainder of 0, the GCF of 32 and 24 is the last non-zero remainder, which is 8.
Division Method
The division method is a straightforward approach to finding the GCF of two numbers. It involves repeatedly dividing the larger number by the smaller number until the remainder becomes 0.
Applying the division method to 32 and 24, we perform the following calculations:
- 32 ÷ 24 = 1.33 (quotient), with a remainder of 8
- 24 ÷ 8 = 3 (quotient), with a remainder of 0
Since the remainder becomes 0, the GCF is the last divisor, which is 8 in this case.
Real-World Applications
The concept of the GCF has wide-ranging applications in various fields. In computer science, the GCF is crucial in optimizing algorithms and data structures. For instance, when designing efficient algorithms for data compression or encryption, understanding the GCF of large integers can lead to significant performance improvements.
In engineering, the GCF plays a vital role in designing mechanical systems. For example, when constructing gear trains, knowing the GCF of gear tooth counts ensures smooth and efficient power transmission.
Additionally, in cryptography, the GCF is a fundamental concept in number theory, which forms the basis for many cryptographic algorithms. The security of cryptographic protocols often relies on the difficulty of factoring large numbers into their prime factors, a process closely related to finding the GCF.
Performance Analysis and Future Implications
The efficiency of GCF calculation methods is a critical aspect for various applications. The prime factorization method, while intuitive, can be computationally expensive for large numbers. On the other hand, the Euclidean algorithm and the division method offer more efficient approaches, especially for larger integers.
In the future, with the ever-increasing demand for computational power and efficiency, optimizing GCF calculation methods will become even more crucial. Researchers and computer scientists are continuously exploring new algorithms and techniques to enhance the performance of GCF calculations, ensuring that these methods remain relevant and effective in the face of evolving technological advancements.
Advanced Techniques
As we delve deeper into the world of GCF calculation, advanced techniques such as the Lehmer’s GCD algorithm and the binary GCD algorithm offer further improvements in computational efficiency. These algorithms leverage the properties of binary numbers and employ more complex mathematical concepts to achieve faster GCF calculations.
For instance, the Lehmer’s GCD algorithm, proposed by Derrick Henry Lehmer in the 1930s, utilizes a recursive approach to calculate the GCD of two numbers. By repeatedly applying the Euclidean algorithm and exploiting the properties of remainders, this algorithm can significantly reduce the number of iterations required to find the GCF.
Similarly, the binary GCD algorithm takes advantage of the binary representation of numbers to perform GCD calculations more efficiently. By converting the numbers into binary format and performing bitwise operations, this algorithm can identify common factors more rapidly, leading to improved performance compared to traditional methods.
| Method | Efficiency | Real-World Use Cases |
|---|---|---|
| Prime Factorization | Moderate | Number Theory, Cryptography |
| Euclidean Algorithm | Highly Efficient | Algorithm Optimization, Data Compression |
| Division Method | Moderate to Efficient | Engineering, Mechanical Systems |

What is the significance of the GCF in computer science and engineering fields?
+
The GCF plays a crucial role in optimizing algorithms, data structures, and mechanical systems. In computer science, it is used to improve efficiency and security in data compression, encryption, and other computational tasks. In engineering, the GCF ensures smooth power transmission in gear trains and other mechanical designs.
Are there any limitations to the GCF calculation methods discussed in this article?
+
While the methods presented are effective for most use cases, they may become less efficient for extremely large integers. In such cases, advanced techniques like the Lehmer’s GCD algorithm and binary GCD algorithm can offer significant improvements in performance.
How can the GCF be applied in cryptography and secure communication?
+
The GCF is a fundamental concept in number theory, which forms the basis for many cryptographic algorithms. Understanding the GCF helps in designing secure cryptographic protocols and ensuring the security of data transmission and storage.



