Mastering the Art of Finding Area Between Curves

The calculation of the area between curves is a fundamental concept in mathematics, often encountered in calculus and geometry. It involves determining the region enclosed by two or more curves and finding its area. While this concept might seem straightforward, it holds a wealth of applications and can be approached through various methods, each with its unique advantages and considerations. In this comprehensive guide, we’ll delve deep into the art of finding the area between curves, exploring different techniques, their underlying principles, and practical applications. Whether you’re a student, a teacher, or a professional in a field that utilizes these calculations, this article aims to provide an in-depth understanding of this essential mathematical skill.
Understanding the Basics: What is the Area Between Curves?
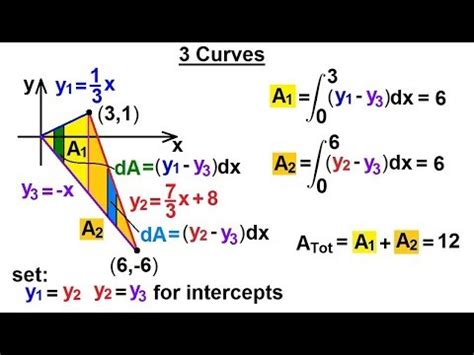
At its core, the area between curves refers to the space enclosed by two or more curves in a two-dimensional plane. This region can be bounded by multiple curves, creating a complex shape, or it can be as simple as the area between two parallel lines. The primary goal is to determine the size of this enclosed region, which is quantified as its area.
The Significance of Finding Area Between Curves
The ability to calculate areas between curves is crucial in various fields. In physics, it’s used to find the mass of an object with varying density, the work done by a variable force, or the electric flux passing through a non-uniform field. Engineers might use it to determine the volume of irregular-shaped tanks or the strength of a beam with a variable cross-section. Economists and statisticians apply these concepts to calculate areas under probability density curves, which have implications for risk analysis and decision-making. Even in the realm of art and design, understanding areas between curves can be instrumental in creating visually appealing shapes and patterns.
Techniques for Calculating the Area Between Curves

There are several methods to determine the area between curves, each suited to different scenarios and offering unique insights. Let’s explore some of these techniques in detail:
Method 1: The Riemann Sum Approach
The Riemann sum method is a foundational technique in calculus, providing a solid framework for understanding the area between curves. This method involves dividing the region between the curves into a series of small rectangles or trapezoids, each with a width of delta x. The height of each rectangle is determined by the function value at a specific point within the interval. By summing up the areas of these small shapes, we approximate the total area between the curves. As we decrease the width of the rectangles, the approximation becomes more accurate, leading to the exact area in the limit.
Advantages of the Riemann Sum Method:
- Fundamental Understanding: This method provides a foundational understanding of the area calculation, laying the groundwork for more advanced techniques.
- Visual Interpretation: The visual representation of the rectangles or trapezoids can help students grasp the concept of area between curves intuitively.
Limitations and Considerations:
- Accuracy vs. Complexity: While the Riemann sum method provides an accurate result in the limit, it can be computationally intensive, especially for complex curves.
- Choice of Points: The method’s accuracy depends on the choice of points within each interval. Different points can lead to different approximations, and selecting the most representative points can be a challenge.
Method 2: Integration and the Fundamental Theorem of Calculus
Integration is a powerful tool in calculus that allows us to find the exact area between curves without relying on approximations. The Fundamental Theorem of Calculus establishes a direct connection between differentiation and integration, providing a systematic way to calculate areas.
Integration Process:
- Identify the Curves: Determine the functions that define the upper and lower boundaries of the region.
- Choose a Bounding Interval: Decide on the interval over which you want to calculate the area.
- Integrate: Use the definite integral to calculate the area. For instance, if the upper curve is given by f(x) and the lower curve by g(x), the area between them from x = a to x = b is given by the integral of f(x) - g(x) from a to b.
Advantages of Integration:
- Exact Results: Integration provides the exact area between curves, eliminating the need for approximations.
- Broad Applicability: This method can be applied to a wide range of curves, from simple linear functions to complex trigonometric and exponential functions.
Considerations:
- Antiderivative Complexity: For some functions, finding the antiderivative can be challenging, especially for non-standard functions.
- Understanding the Integral: It’s essential to grasp the concept of the integral as the accumulation of infinitesimal changes, which can be abstract for beginners.
Method 3: Parametric and Polar Coordinates
In certain situations, especially when dealing with curves that are more easily described in parametric or polar form, these coordinate systems can provide a more natural approach to calculating the area between curves.
Parametric Curves:
For a curve defined by parametric equations x = f(t) and y = g(t), the area between the curve and the x-axis from t = a to t = b can be calculated as the integral of y = g(t) with respect to t from a to b.
Polar Curves:
For a curve defined in polar coordinates as r = f(θ), the area within the curve from θ = a to θ = b is given by the integral of r^2⁄2 with respect to θ from a to b.
Advantages:
- Natural Representation: Parametric and polar coordinates are often more intuitive for describing certain curves, leading to simpler calculations.
- Versatility: These methods can handle curves that might be challenging to express in Cartesian form.
Considerations:
- Additional Complexity: While these methods simplify calculations for specific curves, they introduce new complexities, such as dealing with parametric equations or converting between coordinate systems.
- Limited Applicability: These methods are not universally applicable and are best suited for curves that are naturally described in parametric or polar form.
Method 4: Computer-Assisted Calculations
In today’s digital age, computer software and programming languages offer powerful tools for calculating areas between curves, especially for complex scenarios.
Software Tools:
- Mathematical Software: Programs like MATLAB, Mathematica, or WolframAlpha can perform intricate calculations, offering visual representations and precise results.
- Programming Languages: Languages such as Python, with libraries like SciPy, can be used to implement algorithms for area calculations.
Advantages of Computer-Assisted Calculations:
- Speed and Efficiency: Computers can handle complex calculations with large datasets rapidly, providing results that would be tedious or impossible to obtain manually.
- Flexibility: Computer programs can be tailored to specific problems, accommodating unique curves and constraints.
Considerations:
- Understanding the Underlying Math: It’s essential to have a solid grasp of the mathematical principles to interpret the results correctly.
- Learning Curve: Utilizing these tools effectively requires some proficiency in programming or mathematical software, which can be a barrier for beginners.
Real-World Applications of Area Between Curves
The ability to calculate the area between curves has profound implications in various fields, providing insights and solutions to real-world problems.
Physics:
- Work and Energy: Calculating the area under a force-displacement graph can determine the work done by a variable force.
- Fluid Mechanics: The area between curves is used to find the volume of irregular-shaped tanks or reservoirs.
Engineering:
- Structural Analysis: Engineers use area calculations to determine the strength and stability of structures with variable cross-sections.
- Electrical Engineering: In circuit analysis, the area under a voltage-time graph gives the charge transferred.
Economics and Statistics:
- Risk Analysis: Economists and statisticians use area calculations under probability density curves to assess risk and make informed decisions.
- Demographics: Area calculations are used to understand population distribution patterns, which is crucial for urban planning and resource allocation.
Art and Design:
- Graphic Design: Understanding areas between curves is fundamental for creating visually appealing shapes and patterns in graphic design.
- Architecture: In architecture, area calculations are used to design spaces with unique shapes and structures.
Advanced Topics and Extensions
The concept of area between curves extends far beyond the basics, with numerous advanced topics and applications.
Multiple Integrals and Volume Calculations:
- Double Integrals: By integrating twice, we can calculate the volume under a surface defined by a function of two variables.
- Triple Integrals: Extending this concept further, triple integrals can calculate the volume within a solid defined by a function of three variables.
Applications in Geometry:
- Surface Area of Revolution: Calculating the area between curves can be used to find the surface area created when a curve is rotated about an axis.
- Arc Length: The integral can be used to find the length of a curve, which has applications in physics and engineering.
Probability and Statistics:
- Area Under the Curve: In statistics, the area under a probability density curve represents the probability of an event occurring.
- Confidence Intervals: The concept of area is crucial in determining confidence intervals and making statistical inferences.
Conclusion: A Multifaceted Skill with Endlessly Useful Applications

Mastering the art of finding the area between curves is not just about solving mathematical problems; it’s about developing a skill that can be applied in countless real-world scenarios. From physics and engineering to economics and art, the ability to calculate areas between curves provides a powerful tool for understanding and solving complex problems. Whether you’re a student laying the foundations of your mathematical journey or a professional seeking to deepen your understanding, this guide aims to provide a comprehensive roadmap to navigate the diverse and fascinating world of area calculations.
Key Takeaways:
- The area between curves is a fundamental concept with wide-ranging applications.
- Different methods, from Riemann sums to integration and computer-assisted calculations, offer unique advantages and considerations.
- Real-world applications demonstrate the practical importance of this skill across various fields.
- Advanced topics, such as multiple integrals and probability, further extend the concept’s reach and complexity.
Final Thoughts:
The journey into the art of finding the area between curves is a testament to the beauty and utility of mathematics. It’s a skill that, when mastered, unlocks a deeper understanding of the world around us and empowers us to tackle complex problems with precision and insight.