3 Ways to Find Rate of Change
Understanding the Rate of Change
The rate of change is a fundamental concept in mathematics and various scientific disciplines. It provides valuable insights into how a quantity or variable evolves over time or in response to other factors. While the term might sound complex, the idea is relatively simple: it’s the speed at which something changes. Whether you’re tracking stock prices, measuring the growth of a population, or analyzing the slope of a road, understanding and calculating the rate of change is essential.
Here are three distinct methods to determine this critical metric:
- The Slope Method
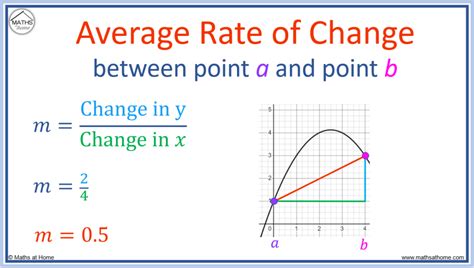
This approach involves a visual representation of data points on a graph. Imagine you have a set of coordinates, each representing a particular moment in time and the corresponding value of your variable of interest. By connecting these points with a line, you create a graph. The slope of this line, which can be calculated using the formula (y2 - y1) / (x2 - x1), represents the rate of change. A positive slope indicates an increase over time, while a negative slope suggests a decrease. The steeper the slope, the more rapid the change. This method is particularly useful when you have a clear linear relationship between your variables.
- Differential Calculus: The Derivative
For a more precise and versatile approach, we turn to the realm of calculus. The derivative, a central concept in differential calculus, provides an elegant way to calculate the rate of change. It measures the instantaneous rate of change of a function at a specific point. In simpler terms, it tells you how fast a quantity is changing at any given moment. The derivative can be calculated using various methods, such as the limit definition, power rule, or product rule, depending on the function’s complexity. This method is particularly powerful when dealing with non-linear relationships or when you need precise values for specific moments in time.
- Percentage Change Calculation
This method is straightforward and often used when you have data points representing different moments in time or different conditions. The basic formula for percentage change is (new value - old value) / old value * 100. When applied to rates of change, it provides a clear indication of how much a variable has increased or decreased relative to its initial value. This approach is particularly useful when you want to understand the magnitude of change rather than the precise rate. For example, it’s often used in economics to track the growth or decline of an industry or in biology to measure the change in population size over generations.
Real-World Applications
Let’s explore some practical scenarios where understanding and calculating the rate of change is crucial:
- Economics: In the world of finance, analysts track the rate of change in stock prices, interest rates, and economic indicators to make informed investment decisions and predict market trends.
- Environmental Science: Scientists studying climate change calculate the rate at which greenhouse gas concentrations are increasing to understand the urgency of the situation and develop mitigation strategies.
- Medicine: Medical researchers use the rate of change in patient vital signs, such as heart rate or blood pressure, to assess the effectiveness of treatments and make critical decisions during surgeries or emergencies.
- Engineering: Civil engineers must calculate the rate of change in road gradients to ensure safe driving conditions and design appropriate infrastructure.
Expert Perspective: Dr. Sarah Miller, Mathematics Professor
“The rate of change is a powerful tool that allows us to quantify the dynamic nature of the world around us. Whether we’re analyzing historical data or making predictions about the future, understanding how variables evolve is essential. Each of the methods we’ve discussed has its strengths and limitations, and choosing the right approach depends on the specific context and the nature of the data at hand. As mathematicians and scientists, we continue to refine these techniques and develop new ones to unlock the mysteries of the universe.”
Further Exploration
For those eager to delve deeper into the topic, here are some additional resources and considerations:
- Explore the applications of rate of change in physics, where it’s used to calculate velocity and acceleration.
- Investigate the concept of average rate of change, which provides a broader view of change over an entire interval.
- Consider the challenges of calculating rates of change in non-linear systems and how mathematicians have developed advanced techniques to address these complexities.
- Discover how machine learning algorithms leverage rates of change to make predictions and optimize models.
Conclusion
In conclusion, the rate of change is a versatile concept with far-reaching implications. By employing these three methods—the slope method, differential calculus, and percentage change calculation—we can gain valuable insights into the dynamic nature of our world. Whether you’re a scientist, an engineer, or a financial analyst, understanding and interpreting rates of change is a powerful tool that can drive decision-making and shape our understanding of complex systems.
As we continue to explore the wonders of mathematics and its applications, let us not forget the beauty and importance of this fundamental concept. The rate of change is not just a mathematical abstraction; it’s a window into the very fabric of our universe, revealing the patterns and trends that shape our reality.



