Mastering Exponential Function: 3 Key Tips
When it comes to mathematics, the exponential function often poses a challenge to many students and even professionals. But with the right approach and understanding, it can be mastered. Here, we delve into the world of exponential functions, offering three crucial tips to help you tackle this mathematical concept with confidence.
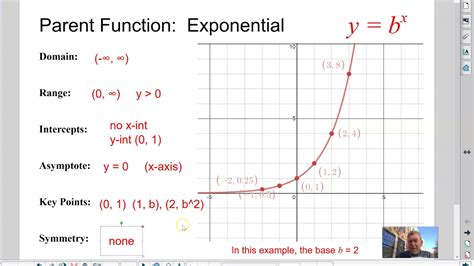
At its core, an exponential function is a mathematical expression where a constant base is raised to a variable power. The base can be any positive number, but the most common ones are 2, e (Euler’s number), and 10. The variable, often denoted as x, determines the exponent or power to which the base is raised. This simple concept can produce some fascinating results, especially when the exponent is a real number or even a complex one.
The beauty of exponential functions lies in their ability to model rapid growth or decay, making them invaluable in various fields like physics, biology, economics, and computer science. For instance, population growth, radioactive decay, compound interest, and even the spread of information on social media can all be modeled using exponential functions.
So, to master this concept, it’s crucial to start with the fundamentals. Here’s a step-by-step breakdown:
- Familiarize yourself with the standard form of an exponential function: f(x) = a^x, where ‘a’ is the base and ‘x’ is the exponent.
- Understand the behavior of different bases. For example, a base greater than 1 (e.g., 2, 3, or 10) will result in exponential growth, while a base between 0 and 1 (e.g., 0.5 or 0.1) will lead to exponential decay.
- Learn how to manipulate exponential functions. This includes operations like adding, subtracting, multiplying, and dividing them, as well as taking their derivatives and integrals.
Step-by-Step Guide to Understanding Basics
- Start with simple exponential functions like 2^x or 10^x.
- Plot these functions on a graph to visualize the growth/decay patterns.
- Experiment with different bases and observe how the curve changes.
- Practice manipulating these functions: add, subtract, multiply, and divide.
- Learn the derivative and integral rules for exponential functions.
- Apply your understanding to real-world examples, such as population growth or financial models.
What is the difference between exponential growth and exponential decay?
+Exponential growth occurs when the base of the exponential function is greater than 1, resulting in a rapid increase in the function's value as the exponent increases. On the other hand, exponential decay happens when the base is between 0 and 1, causing the function's value to decrease rapidly as the exponent increases.
How can I remember which bases represent growth and which represent decay?
+A simple mnemonic is to remember that 'growth' starts with a 'g', just like the numbers greater than 1 (e.g., 2, 3, 10), while 'decay' starts with a 'd', like the numbers between 0 and 1 (e.g., 0.5, 0.1). So, greater than 1 is growth, and between 0 and 1 is decay.
Exponential functions are not just abstract mathematical concepts; they have numerous practical applications across various fields. By exploring these real-world scenarios, you can not only appreciate the relevance of exponential functions but also enhance your understanding and problem-solving skills.
Here are some common areas where exponential functions come into play:
- Population Dynamics: Exponential functions are used to model population growth, helping ecologists, biologists, and sociologists understand how populations change over time.
- Financial Mathematics: Compound interest, a fundamental concept in finance, is based on exponential functions. It’s used to calculate the future value of investments or loans.
- Physics: Exponential functions are essential in physics, particularly in describing the behavior of systems that involve growth or decay, such as radioactive decay, cooling systems, or the spread of heat.
- Computer Science: In computer science, exponential functions are used in algorithms, data structures, and cryptography. For instance, they play a role in calculating the time complexity of certain algorithms.
- Economics: Exponential functions are used in economics to model economic growth, inflation, and depreciation.
By delving into these applications, you can gain a deeper understanding of how exponential functions operate in real-world scenarios. This practical perspective can make learning more engaging and help you retain the concepts better.
Step-by-Step Guide to Exploring Real-World Applications
- Choose a real-world scenario that interests you, such as population growth, financial investments, or the spread of a virus.
- Research how exponential functions are used in that particular scenario.
- Identify the variables involved and how they influence the exponential function.
- Practice applying exponential functions to this scenario using mathematical models.
- Compare your results with real-world data to validate your understanding.
How are exponential functions used in computer science algorithms?
+Exponential functions play a role in analyzing the time complexity of certain algorithms. For instance, in the context of sorting algorithms, an exponential function might be used to describe the worst-case scenario, where the algorithm takes a long time to sort a large number of elements.
Can you give an example of an exponential function used in economics?
+One example is the Solow-Swan model, which is used to model economic growth. It assumes that the growth rate of an economy is proportional to its capital stock, which is often modeled as an exponential function.
Like any mathematical concept, mastering exponential functions requires consistent practice. It’s through repeated application and problem-solving that you’ll truly understand the nuances and intricacies of this concept.
Here are some strategies to incorporate practice into your learning journey:
- Start with Textbook Problems: Work through the exercises provided in your mathematics textbook or online resources. These problems are designed to reinforce your understanding of the concepts and help you apply them in various contexts.
- Explore Online Platforms: There are numerous online platforms that offer practice problems and quizzes on exponential functions. These platforms often provide instant feedback, allowing you to identify and correct your mistakes quickly.
- Real-World Problem Solving: Apply exponential functions to real-world scenarios. This could involve analyzing population growth, calculating compound interest, or predicting the spread of information on social media.
- Collaborate with Peers: Discuss mathematical concepts with your peers. Collaborating with others can provide different perspectives and help you identify areas where you might be struggling.
- Use Technology: Utilize mathematical software or programming languages to explore exponential functions. This can help you visualize the functions, manipulate them, and solve complex problems efficiently.
By incorporating these practice strategies into your learning routine, you’ll not only improve your understanding of exponential functions but also develop valuable problem-solving skills that are transferable to other mathematical concepts.
Step-by-Step Guide to Effective Practice
- Start with basic problems and gradually increase the difficulty level.
- Focus on understanding the underlying concepts rather than just memorizing formulas.
- Use a variety of resources, such as textbooks, online platforms, and real-world scenarios.
- Collaborate with peers and discuss different approaches to problem-solving.
- Keep a record of your progress and identify areas where you need more practice.
- Set realistic goals and celebrate your achievements along the way.
Are there any online platforms that offer practice problems for exponential functions?
+Yes, there are several online platforms that provide practice problems and quizzes on exponential functions. Some popular options include Khan Academy, Mathway, and Wolfram Alpha. These platforms offer a variety of problems with instant feedback, making them great tools for practice.
How can I stay motivated while practicing exponential functions?
+Motivation can be a challenge, especially when dealing with complex mathematical concepts. Here are some tips: set achievable goals, celebrate your progress, find a study partner or group, and take regular breaks to avoid burnout. Additionally, remind yourself of the real-world applications and how your understanding of exponential functions can be valuable in various fields.
Remember, mastering exponential functions is a journey, and with persistence, dedication, and a willingness to explore, you can develop a deep understanding of this fascinating mathematical concept.