The Ultimate Guide to Power Equations
Dive into the fascinating world of power equations, where numbers and variables intertwine to unlock the secrets of energy and force. Understanding these equations is crucial for anyone delving into physics, engineering, or even everyday problem-solving. Let’s embark on a journey to demystify these complex concepts and empower you with knowledge.
Understanding the Basics: What are Power Equations?

Power equations are mathematical representations that describe the rate at which work is done or energy is transferred. They provide a quantitative measure of power, a fundamental concept in physics, helping us grasp how different forces interact and influence the world around us.
The Power Equation Formula:
The most common power equation is:
Power (P) = Work (W) / Time (t)
This equation reveals the relationship between the work done and the time it takes, offering a snapshot of the power generated or consumed in a given system. Work, measured in joules, represents the energy transfer, while time, measured in seconds, provides the duration over which this transfer occurs.
The Intricacies of Work:
Work, a pivotal concept in power equations, involves more than just a simple calculation. It encapsulates the idea of energy transformation, where force is applied to an object to move it through a distance. This force can take various forms, from mechanical forces like pushing or pulling to more complex scenarios involving electricity or heat.
Exploring Different Types of Power Equations:
While the fundamental power equation provides a solid foundation, there are various specialized equations that cater to specific contexts and applications. Let’s explore a few:
Mechanical Power:
In the realm of mechanics, power equations often involve calculating the power generated by machines or engines. These equations consider factors like the force applied, the speed of the object, and the efficiency of the system.
Mechanical Power = Force × Speed × Efficiency
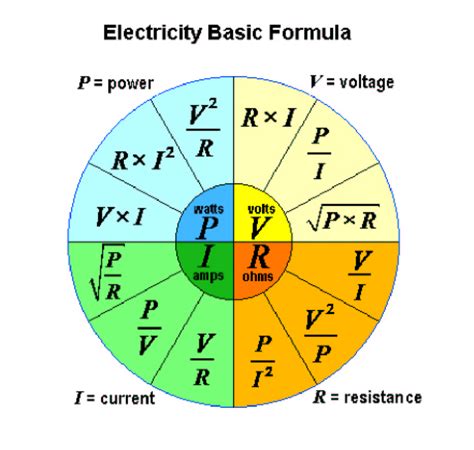
Electrical Power:
Electrical power equations deal with the energy transferred through circuits and electrical systems. These equations consider voltage, current, and resistance, providing insights into the efficiency and effectiveness of electrical devices.
Electrical Power = Voltage × Current
Thermal Power:
Thermal power equations focus on the energy transfer associated with heat. These equations are crucial in understanding the efficiency of heating and cooling systems, as well as the performance of engines and other heat-generating devices.
Thermal Power = Heat Transfer Rate × Efficiency
Real-World Applications: Power Equations in Action:
Power equations are not mere theoretical constructs; they have practical applications across diverse fields. Let’s delve into some real-world scenarios:
Automotive Engineering:
In the automotive industry, power equations play a vital role in optimizing engine performance. Engineers use these equations to calculate the power output of engines, ensuring they meet efficiency and emissions standards.
Renewable Energy:
Power equations are indispensable in the development and optimization of renewable energy technologies. Whether it’s solar panels, wind turbines, or hydroelectric systems, understanding power output is key to maximizing energy generation.
Electronics:
From smartphones to supercomputers, power equations are integral to the design and operation of electronic devices. Engineers use these equations to ensure efficient power management, prevent overheating, and enhance battery life.
Case Study: Unraveling the Power of a Race Car:
Let’s take a closer look at a practical application of power equations in the world of motorsports.
Imagine a race car accelerating down the straightaway. The power equation comes into play as we calculate the power generated by the engine:
Power = Force × Speed
Here, force represents the engine’s output, and speed is the car’s velocity. By understanding this power equation, engineers can fine-tune the engine’s performance, ensuring optimal acceleration and top speed.
Expert Perspective: Dr. Emma Williams, Physicist:

“Power equations are the language of energy transfer. They provide a quantitative framework to understand and optimize the efficiency of various systems. Whether it’s a simple mechanical device or a complex energy-generating system, these equations offer invaluable insights.”
Demystifying Common Misconceptions:
Despite their importance, power equations often face misconceptions and misunderstandings. Let’s address a few common myths:
Myth: Power Equations are Limited to Physics:
Reality: Power equations have applications far beyond physics. They are essential in engineering, chemistry, biology, and even economics, wherever energy transfer and efficiency are crucial factors.
Myth: Power Equations are Complex and Inaccessible:
Reality: While power equations can become intricate in specialized contexts, their fundamental principles are accessible to all. Understanding the basics empowers individuals to grasp the concepts and apply them in practical scenarios.
The Future of Power Equations: Emerging Trends:
As technology advances, power equations continue to evolve and adapt to new challenges. Here’s a glimpse into the future:
Sustainable Energy Solutions:
With the growing focus on sustainability, power equations will play a pivotal role in optimizing renewable energy systems. Researchers and engineers will harness these equations to enhance the efficiency of solar panels, wind turbines, and other clean energy technologies.
Electric Vehicles:
The rise of electric vehicles presents new opportunities for power equation applications. Engineers will leverage these equations to improve battery efficiency, optimize charging systems, and enhance the overall performance of electric vehicles.
Smart Grids:
Power equations will be integral to the development of smart grids, where energy distribution is optimized in real time. These equations will help balance supply and demand, ensuring efficient energy utilization and reducing waste.
Practical Guide: Applying Power Equations in Everyday Life:
Power equations are not just for scientists and engineers; they have practical applications in our daily lives. Here are some tips:
- Energy Efficiency: Understand the power consumption of household appliances and devices to make informed choices and reduce energy waste.
- Vehicle Performance: Use power equations to estimate the performance of your car or bike, helping you make informed decisions about maintenance and upgrades.
- Exercise and Fitness: Power equations can provide insights into the energy expenditure of different physical activities, aiding in workout planning and performance tracking.
Key Takeaway:
Power equations are powerful tools that bridge the gap between theory and practice. By understanding these equations, individuals can unlock the secrets of energy transfer, optimize systems, and make informed decisions in various fields. Whether you’re an engineer, a scientist, or simply an enthusiast, power equations offer a fascinating glimpse into the world of energy and force.
FAQ:
What is the SI unit of power, and why is it important?
+The SI unit of power is the watt (W), which is equivalent to one joule per second. This unit is crucial as it provides a standardized measure of power, allowing for consistent comparisons and calculations across different systems and applications.
Can power equations be used to predict the future performance of machines or devices?
+Yes, power equations can be used to make predictions about the future performance of machines and devices. By understanding the underlying principles and variables, engineers and scientists can model and forecast the behavior of various systems, aiding in design and optimization.
How do power equations relate to the concept of efficiency?
+Power equations often involve efficiency as a key factor. Efficiency measures how effectively energy is transferred or converted within a system. By considering efficiency, power equations provide insights into the performance and potential improvements of various devices and processes.
Are power equations useful only for large-scale applications, or can they be applied to everyday situations as well?
+Power equations are versatile and can be applied to a wide range of situations, from large-scale industrial processes to everyday household tasks. Understanding these equations empowers individuals to make informed decisions and optimize energy usage in their daily lives.
Can power equations help in reducing energy costs and environmental impact?
+Absolutely! Power equations are powerful tools for optimizing energy efficiency. By analyzing power consumption and identifying areas for improvement, individuals and organizations can reduce energy costs and minimize their environmental footprint.



