Unveiling the Dirac Delta Function

The Dirac delta function, often referred to as the impulse function, is a fundamental concept in mathematics and physics, with profound implications across various scientific disciplines. This unique function, despite its seemingly simple definition, has a profound impact on our understanding of signals, systems, and the very nature of the universe. In this article, we delve into the intricacies of the Dirac delta function, exploring its history, mathematical properties, and practical applications.

A Historical Perspective

The story of the Dirac delta function begins in the early 20th century with the groundbreaking work of Paul Dirac, a British theoretical physicist and one of the pioneers of quantum mechanics. Dirac’s eponymous function was introduced as a mathematical construct to describe the behavior of particles at a specific point in space-time, particularly in the context of quantum theory.

However, the origins of the impulse function can be traced back even further. Mathematicians and physicists had long grappled with the concept of an infinitely tall, infinitely thin function, one that could be used to represent an impulse or a point source. The delta function provided a rigorous mathematical framework for this elusive idea.

Mathematical Definition and Properties

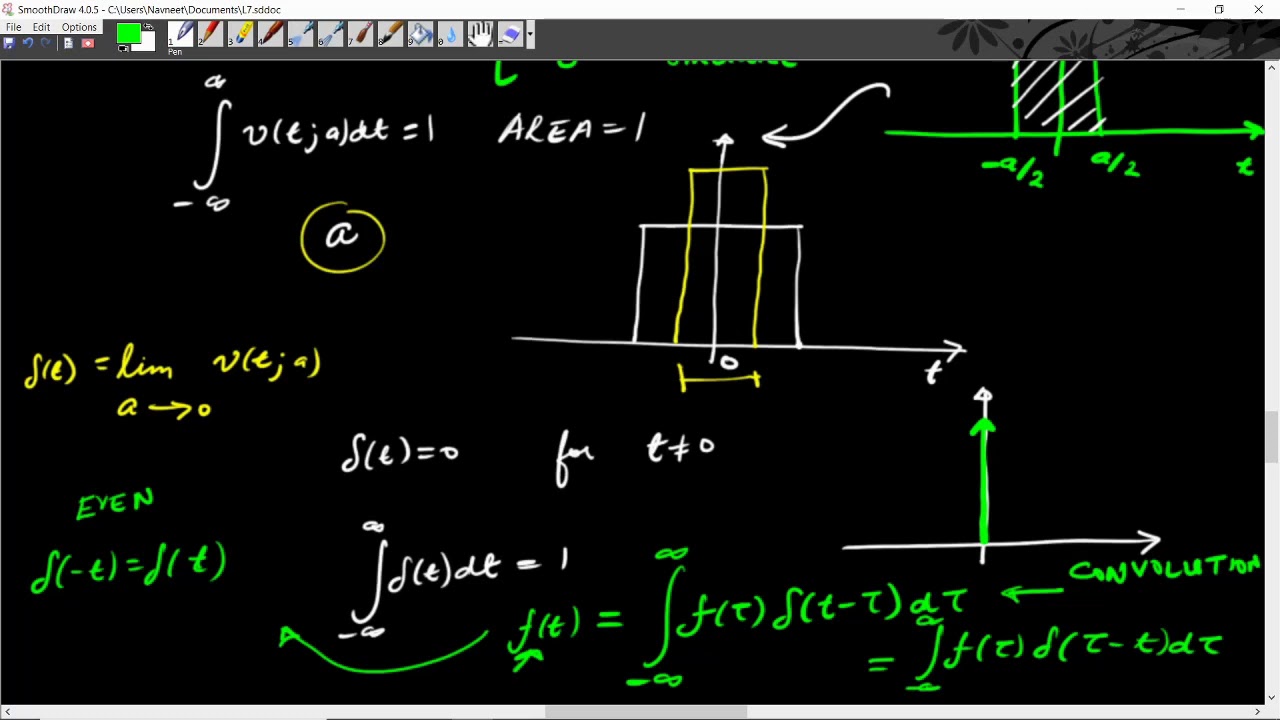
The Dirac delta function, often denoted as δ(x), is defined as a distribution or generalized function. Unlike conventional functions, it is not defined at a single point but rather as a limit of a sequence of functions. Its key property is that it integrates to unity over any interval containing its point of support, while integrating to zero over any interval that does not contain this point.

In simple terms, the Dirac delta function is a mathematical device that allows us to model an impulse or a point source. It is an infinitely tall, infinitely thin function that “picks out” a single point in a given space. This function is not defined in the traditional sense, but rather as a limit of regular functions.

Visualizing the Dirac Delta Function

To grasp the concept of the Dirac delta function, it is helpful to visualize it. Imagine a function that is zero everywhere except at one specific point, where it “spikes” infinitely high. This is the essence of the Dirac delta function.

Applications in Physics and Engineering

The Dirac delta function finds extensive applications in physics and engineering, particularly in signal processing, quantum mechanics, and electromagnetic theory.

In signal processing, the delta function is used to represent impulse responses, which are crucial for understanding how systems respond to input signals. In quantum mechanics, it is employed to describe the wave function of a particle at a specific point in space, providing a fundamental tool for analyzing quantum systems.

Electromagnetic theory also utilizes the delta function to model point charges and point current sources, enabling the analysis of complex electromagnetic fields.

Practical Example: Image Processing

To illustrate the practical applications of the Dirac delta function, let’s consider the field of image processing. In digital imaging, the delta function is used in various techniques, such as convolution and filtering, to enhance or modify images.

For instance, in image sharpening, a convolutional filter with a kernel containing the delta function can be applied to an image. This process enhances the high-frequency components of the image, making it appear sharper.

The Dirac Delta Function in Quantum Mechanics

In quantum mechanics, the Dirac delta function plays a central role in the formulation of the Schrödinger equation, which describes the behavior of quantum systems. The delta function is used to represent the potential energy of a particle in a specific region of space.

Additionally, in quantum field theory, the delta function is employed to describe the interaction between particles, providing a framework for understanding the fundamental forces of nature.

Challenges and Controversies

Despite its widespread use and importance, the Dirac delta function has not been without controversy. Some mathematicians and physicists have questioned its rigorous mathematical foundation, particularly its definition as a distribution.

However, despite these challenges, the delta function has proven to be an invaluable tool, offering a powerful and elegant solution to a wide range of problems in physics and mathematics.

Conclusion

The Dirac delta function, with its unique mathematical properties and profound applications, stands as a testament to the ingenuity and creativity of human intellect. Its ability to describe and analyze phenomena at the fundamental level has shaped our understanding of the universe and continues to drive advancements in various scientific disciplines.

As we continue to explore the complexities of the natural world, the Dirac delta function remains an indispensable tool, offering a bridge between theoretical concepts and practical applications.