The Ultimate Radius-Diameter Guide
In the world of geometry, the relationship between radius and diameter is a fundamental concept that underpins countless mathematical and real-world applications. This guide aims to delve into the intricacies of these two geometric measures, exploring their definitions, formulas, and practical implications. Whether you’re a student, educator, or professional, understanding the radius and diameter is crucial for a wide range of disciplines, from architecture and engineering to physics and computer science.
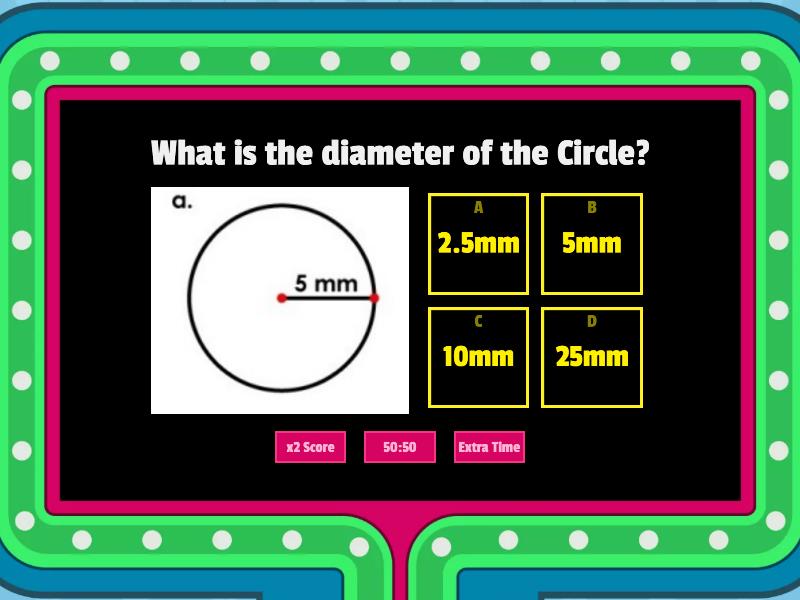
The radius and diameter are two key parameters used to describe the size and shape of circles and spheres. While both measurements are intimately connected, they offer unique perspectives on these geometric figures. The radius, often denoted as ‘r’, is a line segment extending from the center of a circle or sphere to its outer edge. It essentially measures the distance from the center to the circumference. On the other hand, the diameter, symbolized as ’d’, represents a line segment that passes through the center of a circle or sphere and terminates at two opposite points on the circumference. It essentially measures the widest distance across the circle or sphere.
The radius and diameter are like two sides of the same coin, offering distinct yet complementary views of the same geometric entity.
Defining Radius and Diameter
Radius
The radius is a critical geometric parameter that defines the distance from the center of a circle or sphere to its outer boundary. It essentially provides a measure of the circle’s or sphere’s ‘radius of action,’ indicating how far the influence or effect extends from the center. In a 2D context, the radius describes the distance from the center to any point on the circle’s circumference. In a 3D context, the radius measures the distance from the center to any point on the sphere’s surface.
Mathematically, the radius is defined as:
\[ \begin{equation*} \text{Radius} = \frac{\text{Diameter}}{2} \end{equation*} \]
This equation highlights the inverse relationship between the radius and diameter. A circle or sphere with a larger radius will have a proportionally larger diameter, and vice versa.
Diameter
The diameter, in contrast, represents the widest distance across a circle or sphere, passing through the center. It essentially measures the ‘width’ of the geometric figure, providing a sense of its overall size and extent. In a 2D context, the diameter describes the distance between two opposite points on the circle’s circumference, passing through the center. In a 3D context, the diameter measures the distance between two opposite points on the sphere’s surface, again passing through the center.
Mathematically, the diameter is defined as:
\[ \begin{equation*} \text{Diameter} = 2 \times \text{Radius} \end{equation*} \]
This equation emphasizes the direct relationship between the diameter and radius. A circle or sphere with a larger diameter will have a proportionally larger radius, and a smaller diameter will have a proportionally smaller radius.
Practical Applications
The concepts of radius and diameter have wide-ranging practical applications across various fields. Here are some key areas where these geometric measures play a crucial role:
Architecture and Engineering
In architecture and engineering, the radius and diameter are fundamental to designing structures like domes, arches, and curved surfaces. For example, in the design of a dome, the radius of the dome’s base determines the overall shape and size of the structure, while the diameter defines the widest point across the dome, influencing its architectural and structural integrity.
Physics and Astronomy
In physics, the radius and diameter are essential for understanding the properties of spherical objects like planets, stars, and atoms. For instance, the radius of an atom’s nucleus determines the overall size of the atom, while the diameter of a planet or star provides insights into its volume, mass, and other physical characteristics.
Computer Graphics and 3D Modeling
In computer graphics and 3D modeling, the radius and diameter are critical for creating realistic and accurate virtual environments. For example, when modeling a sphere, the radius determines the size and shape of the object, while the diameter defines its overall width and the placement of key features like texture coordinates.
Formulas and Calculations
Understanding the radius and diameter also involves familiarity with various formulas and calculations that utilize these geometric measures. Here are some key formulas involving radius and diameter:
Circumference of a Circle
The circumference of a circle, denoted as ‘C’, is the distance around the circle’s outer boundary. It is calculated using the formula:
\[ \begin{equation*} \text{Circumference} = 2 \times \pi \times \text{Radius} \end{equation*} \]
or, using the diameter:
\[ \begin{equation*} \text{Circumference} = \pi \times \text{Diameter} \end{equation*} \]
where ‘π’ (pi) is a mathematical constant approximately equal to 3.14159.
Area of a Circle
The area of a circle, denoted as ‘A’, represents the region enclosed by the circle’s circumference. It is calculated using the formula:
\[ \begin{equation*} \text{Area} = \pi \times \text{Radius}^2 \end{equation*} \]
or, using the diameter:
\[ \begin{equation*} \text{Area} = \frac{\pi \times \text{Diameter}^2}{4} \end{equation*} \]
Volume of a Sphere
The volume of a sphere, denoted as ‘V’, represents the three-dimensional space enclosed by the sphere’s surface. It is calculated using the formula:
\[ \begin{equation*} \text{Volume} = \frac{4}{3} \times \pi \times \text{Radius}^3 \end{equation*} \]
or, using the diameter:
\[ \begin{equation*} \text{Volume} = \frac{\pi \times \text{Diameter}^3}{6} \end{equation*} \]
Radius vs. Diameter: A Comparative Analysis
While the radius and diameter are closely related, they offer distinct perspectives on the size and shape of circles and spheres. Here’s a comparative analysis of these two geometric measures:
| Radius | Diameter |
|---|---|
| Measures the distance from the center to the circumference | Measures the widest distance across the circle or sphere |
| Smaller in value compared to the diameter | Larger in value compared to the radius |
| Inverse relationship with diameter | Direct relationship with radius |
| Used in 2D and 3D contexts | Used in 2D and 3D contexts |
| Essential for understanding the circle’s or sphere’s ‘radius of action’ | Provides insights into the overall size and extent of the geometric figure |

Real-World Examples

Let’s explore some real-world examples to illustrate the practical applications of radius and diameter:
Earth’s Radius and Diameter
The Earth, our planet, is an excellent example of a spherical object with a defined radius and diameter. The Earth’s radius is approximately 6,371 kilometers (3,959 miles), and its diameter is approximately 12,742 kilometers (7,918 miles). These measurements are critical for understanding Earth’s size, shape, and gravitational characteristics.
Soccer Ball Radius and Diameter
A soccer ball, with its iconic spherical shape, also exhibits radius and diameter characteristics. The radius of a standard soccer ball is approximately 11 inches, and its diameter is approximately 22 inches. These measurements are crucial for designing and manufacturing soccer balls that meet international standards and provide optimal performance during play.
Wheel Radius and Diameter
The radius and diameter of wheels are essential parameters in various transportation systems. For example, the radius of a car wheel determines the overall size of the wheel and influences factors like ground clearance and handling. The diameter of the wheel, which is twice the radius, defines the width of the wheel and affects aspects like tire size and compatibility.
Historical Perspective
The concepts of radius and diameter have a rich historical context, dating back to ancient civilizations that made significant contributions to mathematics and geometry. The ancient Greeks, for instance, made notable advancements in geometry, including the development of the concept of a circle’s radius and diameter. Greek mathematicians like Euclid and Archimedes explored these geometric measures in their mathematical treatises, laying the foundation for modern geometric understanding.
Future Trends and Innovations
As technology and scientific understanding continue to advance, the concepts of radius and diameter are likely to play an increasingly prominent role in various fields. For example, in the field of nanotechnology, the precise control of radius and diameter measurements is crucial for developing nanoscale materials and devices with unique properties. In astronomy, more accurate measurements of celestial objects’ radii and diameters are essential for understanding their formation, evolution, and potential habitability.
Conclusion
In conclusion, the radius and diameter are fundamental geometric measures that offer a wealth of insights into the size, shape, and properties of circles and spheres. Understanding these concepts is crucial for a wide range of disciplines, from architecture and engineering to physics and computer science. By exploring the definitions, formulas, and practical applications of radius and diameter, we gain a deeper appreciation for the mathematical elegance and real-world significance of these geometric measures.
The radius and diameter are essential geometric parameters with far-reaching implications across various fields, offering a powerful lens through which to understand and interact with the world around us.