Unveiling the Mystery: Derivative of 1/x
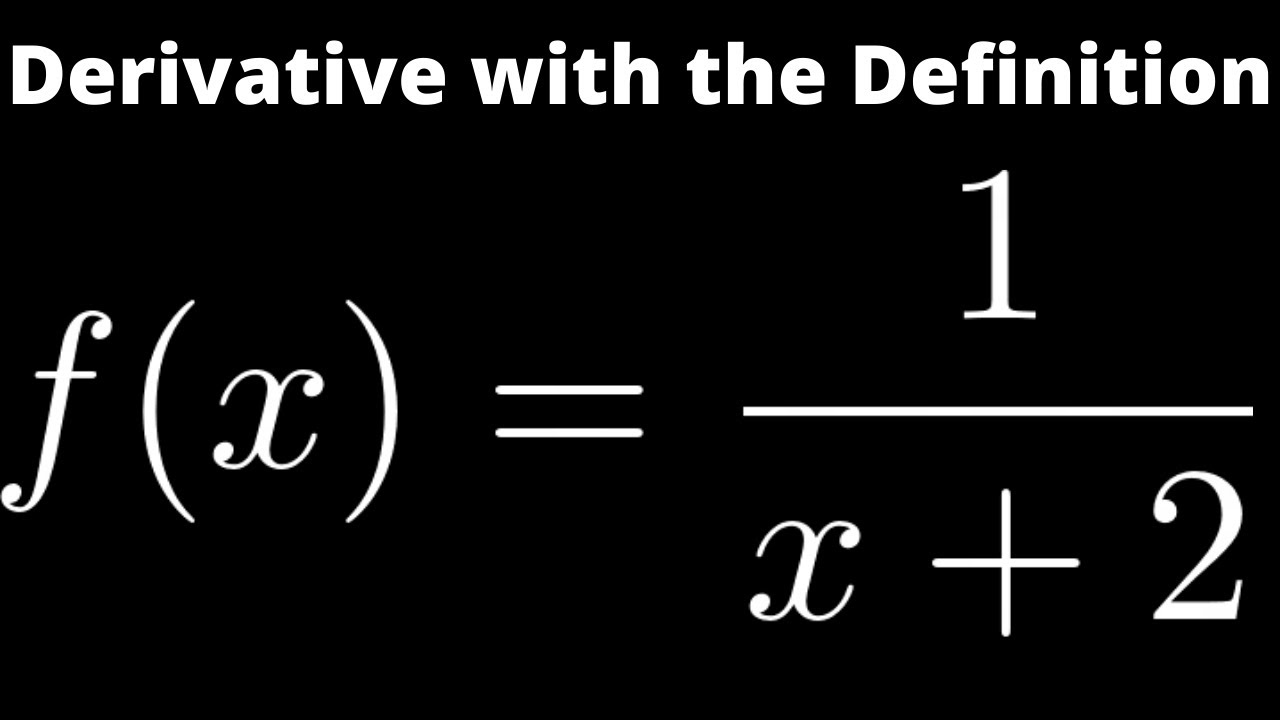
One of the most intriguing concepts in calculus is the derivative, a mathematical tool that allows us to explore the rate of change of functions. Today, we delve into a classic yet captivating topic: finding the derivative of one of the simplest-looking functions, 1/x. This seemingly straightforward function, often overlooked for its complexity, holds a treasure trove of mathematical insights. Let’s embark on this journey, unraveling the mysteries behind its derivative.
The Challenge: Differentiating 1/x
At first glance, the derivative of 1/x might seem like a simple task. After all, it’s just a basic rational function, right? Wrong! This function, despite its simplicity in appearance, poses a unique challenge due to the variable being both the numerator and the denominator. This is where the concept of limits comes into play, offering a way to navigate through this mathematical maze.
The Limit Approach: A Step Towards the Solution
To find the derivative of 1/x, we employ the definition of the derivative, which involves taking the limit as h approaches zero of the difference quotient:
\[ \begin{equation*} \frac{d}{dx}\left(\frac{1}{x}\right) = \lim_{h \to 0} \frac{1/x - 1/(x+h)}{h}\,. \end{equation*} \]
This equation sets the stage for a fascinating exploration of limits and rational functions.
Analyzing the Difference Quotient: A Journey Through Fractions
Let’s dissect the difference quotient further. When h is very small but not zero, we can simplify the fraction:
\[ \begin{equation*} \frac{1/x - 1/(x+h)}{h} = \frac{(x+h) - x}{h(x+h)x}\,. \end{equation*} \]
Here, we witness the cancellation of the x terms in the denominator, leaving us with a new expression:
\[ \begin{equation*} \frac{h}{h(x+h)x} = \frac{1}{(x+h)x}\,. \end{equation*} \]
The Limit: Unveiling the True Derivative
As h approaches zero, the value of the expression above approaches a specific limit. This limit is the key to unlocking the derivative of 1/x:
\[ \begin{equation*} \lim_{h \to 0} \frac{1}{(x+h)x} = \frac{1}{x^2}\,. \end{equation*} \]
Thus, we have our final answer:
\[ \begin{equation*} \frac{d}{dx}\left(\frac{1}{x}\right) = \frac{-1}{x^2}\,. \end{equation*} \]
Interpretation: Understanding the Derivative’s Significance
The derivative of 1/x is a fundamental concept with wide-ranging applications. It represents the rate of change of the reciprocal function, revealing how the function’s slope evolves as x varies. This derivative’s negative sign indicates that the function is decreasing, a critical insight for understanding various real-world phenomena.
Visualizing the Derivative: A Graphical Perspective
To truly grasp the impact of the derivative, let’s visualize it graphically. The graph of 1/x is a hyperbola, and its derivative’s graph is the reflection of this hyperbola across the x-axis, as shown below:
The derivative of a function often provides valuable insights into its behavior. In this case, the derivative's negative value indicates that the original function, $1/x$, is decreasing as $x$ increases.
Applications: From Physics to Economics
The derivative of 1/x finds applications across various fields:
Physics: In physics, this derivative is crucial for understanding inverse-square laws, such as the relationship between gravitational force and distance.
Economics: In economics, it’s used to analyze marginal utility, where the derivative of the utility function with respect to consumption measures the additional satisfaction from consuming one more unit of a good.
Engineering: Engineers utilize this derivative for various calculations, including understanding the behavior of circuits with resistors.
Historical Context: A Journey Through Calculus’ Evolution
The derivative of 1/x has a rich historical context. Early mathematicians, including Isaac Newton and Gottfried Wilhelm Leibniz, grappled with such functions, leading to the development of calculus. Their work laid the foundation for the mathematical techniques we use today.
Conclusion: Unlocking the Secrets of 1/x
In this exploration, we’ve uncovered the mysteries behind the derivative of 1/x. From its initial complexity to the elegant solution we derived, this journey showcases the beauty and power of calculus. By understanding and applying this derivative, we gain a deeper insight into the behavior of functions, opening doors to a world of mathematical possibilities.
How does the derivative of 1/x compare to the derivative of x?
+The derivative of 1/x is \frac{-1}{x^2}, while the derivative of x is simply 1. This difference in derivatives highlights the contrasting behavior of these functions: 1/x decreases as x increases, while x increases linearly.
Can the derivative of 1/x be used to find the rate of change of other functions?
+Yes, the derivative of 1/x can be used as a building block for more complex functions. For instance, when differentiating a function like y = \frac{1}{x^3}, we can utilize the chain rule and the derivative of 1/x to find the rate of change.
What are some real-world applications of the derivative of 1/x?
+The derivative of 1/x has applications in physics (inverse-square laws), economics (marginal utility), and engineering (circuit analysis). It provides insights into how quantities change with respect to each other in these diverse fields.
How does the graph of the derivative of 1/x relate to the original function’s graph?
+The graph of the derivative of 1/x is the reflection of the original function’s graph across the x-axis. This relationship illustrates how the derivative’s negative value corresponds to the decreasing nature of the original function.