The Ultimate Guide to Differentiating 0

Unraveling the Enigma of Zero: A Comprehensive Exploration

In the vast landscape of mathematics, a single digit stands as a cornerstone, yet it often goes unnoticed or misunderstood. Zero, a seemingly simple concept, holds immense power and complexity. It is the absence, the void, and yet, it defines the presence of numbers, shapes, and quantities. In this guide, we embark on a journey to unravel the layers of this enigmatic digit, exploring its historical evolution, mathematical significance, and practical applications.

The concept of zero has a rich and diverse history, stretching across civilizations and epochs. It emerged independently in various cultures, each contributing unique perspectives to its understanding. From the ancient Babylonians, who used a placeholder symbol, to the Indian mathematicians who introduced the concept of “sunya,” zero’s journey is a testament to humanity’s quest for numerical precision.

Historical Timeline:

• Ancient Civilizations: The earliest hints of zero’s existence can be traced back to the ancient Egyptians, who used a symbol resembling a small circle to denote the absence of quantity.
• Babylonian Contributions: Around 300 BCE, the Babylonians advanced the concept with their base-60 number system, utilizing a space as a placeholder.
• Indian Mathematics: In the 5th century CE, Indian mathematicians revolutionized zero, treating it as a number with its own identity and rules. This innovation laid the foundation for modern mathematics.
• European Acceptance: The concept of zero faced resistance in Europe, with some viewing it as a philosophical conundrum. It wasn’t until the 12th century that European scholars, influenced by Arabic texts, embraced zero as a numerical entity.

Mathematical Significance and Applications

Zero is not merely a placeholder or an absence; it is a fundamental concept with far-reaching implications. In mathematics, it serves as the origin point, the reference from which all other numbers are measured. Its unique properties make it an essential tool in various mathematical disciplines.

Algebraic Mastery:

• Solving Equations: Zero is pivotal in equation solving. It helps identify roots, intersections, and critical points, allowing mathematicians to unravel complex problems.
• Polynomials and Functions: The study of polynomials and their behaviors heavily relies on the concept of zero. It helps determine the number of real roots and the nature of the function’s graph.
• Modular Arithmetic: In this branch of mathematics, zero plays a crucial role, serving as the remainder when dividing numbers. It enables the study of patterns and relationships in number systems.

Geometric Explorations:

• Coordinate Systems: Zero is the origin in Cartesian coordinate systems, providing a reference point for plotting points and shapes.
• Angles and Directions: In geometry, zero degrees mark the starting point for measuring angles. It facilitates the understanding of rotations and directions.
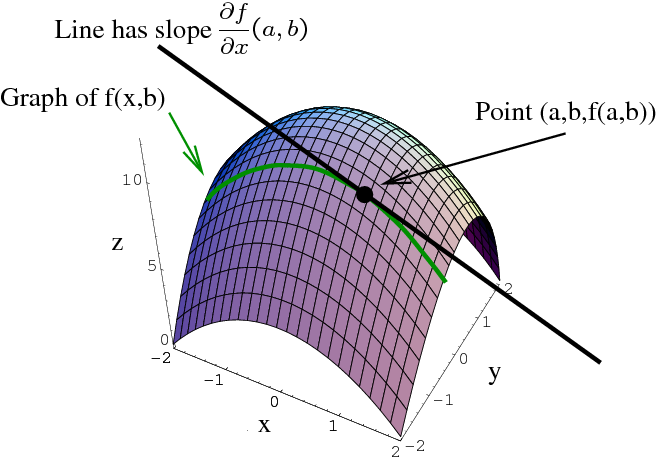
• Calculus and Limits: As the foundation of calculus, zero’s role is crucial. It helps define limits, derivatives, and integrals, enabling the study of change and motion.

Zero in Practical Applications

Beyond its mathematical significance, zero finds applications in various real-world scenarios, often going unnoticed yet critical to our daily lives.

Financial Management:

• Accounting: Zero is the baseline for financial transactions. It signifies the absence of value, ensuring accurate record-keeping and balance sheets.
• Budgeting: When budgeting, zero-based budgeting is a popular approach, where every expense must be justified, ensuring optimal financial planning.

Scientific Precision:

• Measurement: In scientific experiments, zero is the reference point for measurements. For instance, zero degrees Celsius is the freezing point of water, a critical reference in temperature measurements.
• Precision Instruments: Many instruments, from thermometers to scales, rely on zero as the starting point, ensuring accurate readings.

Technological Advancements:

• Binary Code: In the digital world, zero is a fundamental digit in binary code, forming the basis of all digital information and communication.
• Error Correction: Zero plays a role in error-correcting codes, ensuring data integrity and reliable transmission.

Conclusion: The Power of Nothingness

As we delve deeper into the world of zero, its simplicity belies a profound complexity. It is a concept that has shaped the evolution of mathematics and continues to influence our understanding of numbers, quantities, and the very fabric of our universe. From its historical emergence to its modern-day applications, zero remains a testament to humanity’s relentless pursuit of knowledge and precision.

In the grand tapestry of mathematics, zero stands as a silent yet powerful thread, weaving together the very essence of our numerical understanding.