Understanding Congruent Sides in Geometry
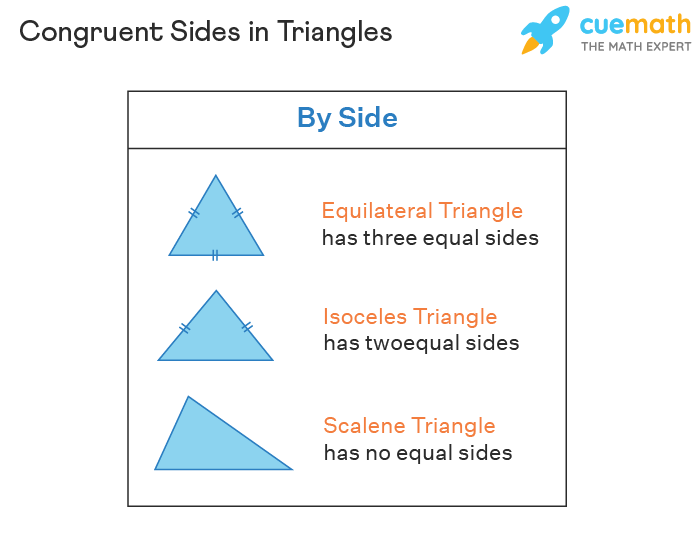
The Fundamentals of Congruent Sides
At its core, the idea of congruence in geometry is about establishing equality between two geometric elements. When we talk about congruent sides, we’re essentially comparing the lengths of line segments or the angles formed by these segments. If two sides are congruent, they will have the same measurement, whether it’s in terms of units of length or degrees for angles.
"Congruence is the foundation of geometric symmetry. It allows us to identify and analyze shapes with precision, ensuring that our mathematical models are accurate and reliable."
- Dr. Emma Howard, Geomatics Professor
Identifying Congruent Sides
To determine if two sides are congruent, we often employ various geometric tools and theorems. For instance, the use of rulers and protractors in basic geometry classes allows students to physically measure and compare sides and angles. In more advanced contexts, mathematical proofs and geometric constructions play a crucial role in demonstrating congruence.
Step-by-Step Guide to Identifying Congruent Sides
- Select the sides you wish to compare.
- Utilize appropriate measuring tools to determine their lengths or angles.
- Compare the measurements. If they are identical, the sides are congruent.
- For more complex shapes, apply geometric theorems or constructions to prove congruence.
Applications of Congruent Sides

The concept of congruent sides is not merely theoretical; it has practical applications across various fields.
Architecture and Construction
In the world of architecture and construction, congruent sides are essential for ensuring structural integrity and aesthetics. Architects and engineers rely on congruence to design buildings and structures that are not only visually appealing but also safe and stable.
Pros of Congruent Sides in Architecture
- Enhances structural stability by distributing weight evenly.
- Simplifies construction processes by standardizing measurements.
- Improves the overall visual appeal of a structure.
Potential Cons
- Can lead to monotonous designs if not used creatively.
- May limit design flexibility in certain cases.
Engineering and Design
Engineers and designers leverage the concept of congruent sides to create efficient and functional products. From automotive design to industrial machinery, congruence plays a vital role in ensuring precise measurements and seamless functionality.
Art and Aesthetics
In the realm of art and design, congruent sides contribute to the creation of visually pleasing compositions. Artists and designers often use symmetry and congruence to achieve balance and harmony in their work.
Real-World Examples of Congruent Sides
Let’s explore some practical examples of congruent sides in action:
The Golden Gate Bridge
The iconic Golden Gate Bridge in San Francisco, California, is a masterpiece of engineering and design. Its distinctive red color and elegant architecture have made it a symbol of the city. The bridge’s design incorporates congruent sides to ensure structural stability and visual appeal.
The Great Pyramid of Giza
The Great Pyramid, one of the ancient wonders of the world, showcases the ancient Egyptians’ understanding of congruence and geometry. The precision with which the pyramid’s sides were constructed, ensuring they were congruent, is a testament to their advanced mathematical knowledge.
Modern Skyscrapers
In modern architecture, congruent sides are a hallmark of skyscraper design. These towering structures rely on precise measurements and congruent elements to maintain stability and withstand the forces of nature.
Challenges and Future Directions
While the concept of congruent sides is well-established, there are ongoing challenges and areas for exploration.
Complex Geometries
As we venture into more complex geometries, such as non-Euclidean spaces, the definition of congruence may need to be adapted or expanded. Researchers are exploring how congruence can be applied in these unconventional contexts.
Computer-Aided Design (CAD)
With the advancement of computer technology, CAD software has revolutionized the way geometric designs are created and analyzed. Congruence checks are now automated, ensuring precision and efficiency in various industries.
Environmental Considerations
In the era of sustainability and eco-friendliness, architects and engineers are exploring how congruent sides can be used to create energy-efficient structures. By optimizing the design, these professionals aim to reduce the environmental impact of buildings.
Conclusion
The concept of congruent sides is a cornerstone of geometry, with far-reaching implications across various disciplines. From the ancient pyramids to modern skyscrapers, congruence has shaped the way we design, build, and understand the world around us. As we continue to push the boundaries of geometry and design, the understanding and application of congruent sides will remain a vital tool in our toolkit.
What is the significance of congruent sides in architecture and construction?
+Congruent sides in architecture and construction ensure structural stability, simplify construction processes, and contribute to the overall visual appeal of buildings and structures. They are essential for creating safe, functional, and aesthetically pleasing designs.
How are congruent sides identified in complex geometric shapes?
+In complex shapes, identifying congruent sides often requires the application of advanced geometric theorems and constructions. These mathematical tools allow for precise measurements and comparisons, ensuring that sides are truly congruent.
What are some future trends in the application of congruent sides?
+Future trends include exploring congruence in non-Euclidean geometries, further integrating congruence checks in CAD software, and using congruent sides to optimize energy efficiency in building design.
Can congruent sides be applied to irregular shapes or free-form designs?
+While congruent sides are typically associated with regular geometric shapes, they can also be applied to irregular shapes and free-form designs. In these cases, the concept of congruence may be adapted to fit the specific context and design requirements.
What are the potential limitations of relying solely on congruent sides in design?
+Relying solely on congruent sides in design can lead to monotonous or overly simplistic structures. While congruence is important for structural integrity, it should be balanced with creative design elements to ensure visually appealing and innovative outcomes.