Calculate Cylinder Volume with Ease
Calculating the volume of a cylinder is a fundamental task in geometry and physics, often required in various real-world applications. Whether you’re designing mechanical components, analyzing fluid dynamics, or simply curious about the capacity of cylindrical objects, this process is both essential and surprisingly simple.
To calculate the volume of a cylinder, you need to consider two key dimensions: the height (h) and the radius ® of the base. These values, along with a mathematical constant known as pi (π), form the basis of the formula for cylindrical volume.
The Formula for Cylindrical Volume
The formula for calculating the volume of a cylinder is straightforward:
\[ \begin{equation*} V = \pi \cdot r^2 \cdot h \end{equation*} \]
Here, V represents the volume, \pi is the mathematical constant approximately equal to 3.14159, r is the radius of the base, and h is the height of the cylinder.
Step-by-Step Calculation Process

Now, let’s break down the calculation process into simple steps:
Measure the Radius: Start by determining the radius of the cylinder’s base. The radius is the distance from the center of the base to its edge. Ensure that you measure in the same unit of length as you will use for the height.
Measure the Height: Next, measure the height of the cylinder. This is the vertical distance from one base to the other.
Square the Radius: Calculate the square of the radius (r^2). This involves multiplying the radius by itself.
Multiply by Pi: Multiply the squared radius by the value of pi (\pi). This gives you the area of the base multiplied by the height.
Multiply by Height: Finally, multiply the result from step 4 by the height of the cylinder. This completes the calculation, giving you the volume of the cylinder.
Example Calculation
Let’s illustrate this process with an example. Imagine you have a cylinder with a radius of 5 cm and a height of 10 cm.
- Radius: r = 5 cm
- Height: h = 10 cm
- Squared Radius: r^2 = 5^2 = 25 cm^2
- Multiply by Pi: 25 \text{ cm}^2 \times \pi \approx 25 \text{ cm}^2 \times 3.14159 \approx 78.54 cm^2
- Multiply by Height: 78.54 \text{ cm}^2 \times 10 \text{ cm} \approx 785.4 cm^3
So, the volume of this cylinder is approximately 785.4 cubic centimeters.
Practical Applications
Understanding how to calculate cylindrical volume has numerous practical applications:
Manufacturing: Engineers and designers need to calculate the volume of cylindrical parts and containers to ensure they meet specifications and function as intended.
Packaging and Storage: Companies in the packaging industry use cylindrical volume calculations to determine the optimal size of containers for products, ensuring efficient use of space and materials.
Architecture and Construction: Architects and builders may need to calculate the volume of cylindrical structures like silos, tanks, or even pillars, to ensure structural integrity and optimal use of resources.
Science and Research: Researchers in fields like fluid dynamics, materials science, and environmental science often rely on cylindrical volume calculations to analyze and predict the behavior of various substances and systems.
Variations and Extensions

While the basic formula for cylindrical volume is simple, there are variations and extensions that can be useful in certain contexts:
Partial Cylinder Volume: If you only have a portion of a cylinder, you can adjust the formula to calculate the volume of that section.
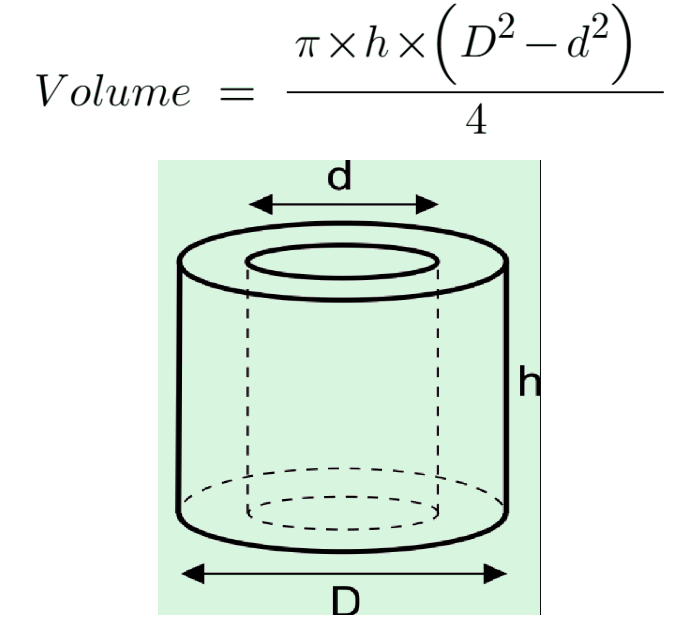
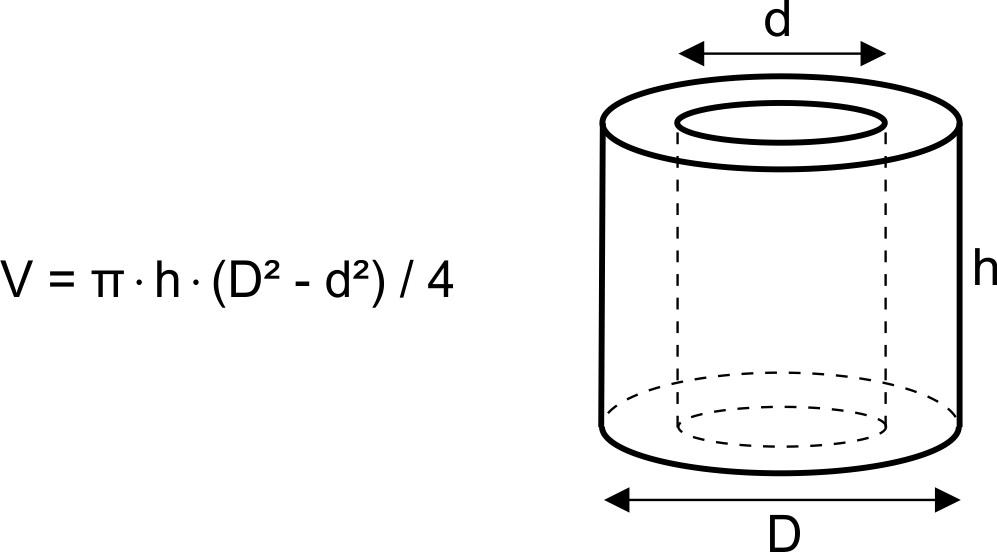
Hollow Cylinder Volume: For hollow cylindrical objects, you can calculate the volume of the inner and outer cylinders separately and then subtract the inner volume from the outer volume to find the hollow cylinder’s volume.
Conical Frustum Volume: A conical frustum, which is essentially a truncated cone, can be treated as a difference between two cylinders with different radii and heights, allowing for its volume to be calculated.
Accuracy and Precision
To ensure accurate volume calculations, it’s essential to measure the radius and height precisely. Even small errors in measurement can lead to significant discrepancies in the calculated volume.
Additionally, when working with real-world applications, it’s important to consider the context and constraints. For instance, if you’re calculating the volume of a cylindrical tank, you might need to account for factors like the thickness of the tank walls or the presence of internal structures.
Conclusion
Calculating the volume of a cylinder is a fundamental skill in mathematics and various scientific and engineering disciplines. By understanding the basic formula and its variations, you can easily determine the capacity of cylindrical objects, which is crucial for a wide range of practical applications.
Remember, while the process is simple, precision and attention to detail are key to accurate results. With this knowledge, you’re now equipped to tackle a multitude of volume-related problems and contribute to a wide array of fields that rely on cylindrical calculations.



