Unveiling the Secrets of a Perfect Bell Curve

In the world of statistics and data analysis, the bell curve, also known as the normal distribution, is a ubiquitous and fundamental concept. It is a powerful tool that allows us to understand and interpret a wide range of phenomena, from the distribution of heights in a population to the performance of students in an exam. This article aims to delve deep into the secrets of the perfect bell curve, exploring its characteristics, applications, and the insights it provides.
Understanding the Bell Curve: A Mathematical Beauty

The bell curve, a graceful and symmetrical curve, represents a probability distribution that occurs naturally in many real-world scenarios. It is characterized by its unique shape, resembling a bell, with a single peak at the center and gradually decreasing tails on both sides. This curve is defined by a set of mathematical equations, where the mean, standard deviation, and other parameters govern its shape and position.
One of the key attributes of the bell curve is its symmetry. The mean, median, and mode all coincide at the center of the distribution, creating a perfectly balanced and aesthetically pleasing curve. This symmetry is not only visually appealing but also signifies that the data points are evenly distributed around the central value, making it a reliable indicator of typical or average behavior.
Key Characteristics of the Bell Curve
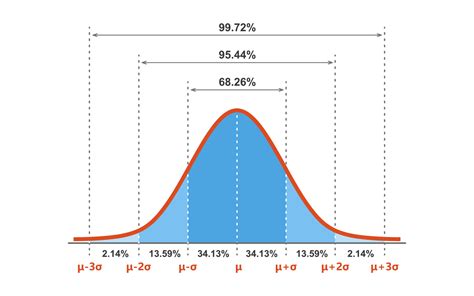
- The bell curve is unimodal, meaning it has a single peak, indicating that the majority of data points are clustered around the mean.
- It is symmetric about the mean, with both tails extending equally in opposite directions.
- The curve is smooth and continuous, without any abrupt changes or discontinuities.
- The area under the curve represents the probability of observing a particular value, and it sums up to 1.
- The bell curve is described by two parameters: the mean (μ) and the standard deviation (σ), which determine its position and spread.
| Characteristic | Description |
|---|---|
| Mean | The average value of the distribution, representing the central tendency. |
| Standard Deviation | A measure of variability, indicating how much the data points deviate from the mean. |
| Skewness | A measure of asymmetry, indicating whether the distribution is skewed to the left or right. |
| Kurtosis | A measure of the "peakedness" of the distribution, indicating how tall and narrow or flat and wide it is. |

Applications of the Bell Curve in Real-World Scenarios
The bell curve finds extensive applications across diverse fields, offering valuable insights and predictions. Here are some real-world scenarios where the bell curve plays a crucial role:
1. Academic Performance Assessment
In educational settings, the bell curve is often used to evaluate student performance. Exam scores or grades are typically distributed along a bell curve, with most students scoring around the mean and fewer students scoring at the extremes. This distribution helps educators understand the typical range of student abilities and identify outliers or exceptional performers.
For example, consider a class of 100 students who take a standardized exam. The bell curve can be used to visualize the distribution of their scores, with the majority clustering around the mean and a few students scoring exceptionally high or low. This distribution allows teachers to set realistic expectations, identify areas for improvement, and design targeted interventions.
2. Quality Control in Manufacturing
In the manufacturing industry, the bell curve is a vital tool for quality control and process optimization. By analyzing the distribution of product characteristics, such as weight, dimensions, or color, manufacturers can identify defects, improve production processes, and ensure consistent quality.
Imagine a factory producing electronic components. The bell curve can be used to assess the distribution of component sizes, with the mean representing the ideal size. Deviations from the mean can indicate potential issues, such as faulty machinery or inconsistent materials, allowing the manufacturer to take corrective actions and maintain product quality.
3. Financial Market Analysis
In the world of finance, the bell curve is used to model and predict stock prices, interest rates, and other financial variables. By understanding the distribution of these variables, investors and analysts can make informed decisions, assess risks, and develop trading strategies.
For instance, an investment firm might analyze the historical distribution of stock returns to identify the typical range of returns and assess the probability of extreme events. This information helps them allocate resources, manage risk, and develop investment plans.
4. Social Sciences Research
The bell curve is a valuable tool in social sciences, such as sociology, psychology, and economics. It allows researchers to understand and model human behavior, attitudes, and preferences. By analyzing the distribution of survey responses, test scores, or demographic data, researchers can draw meaningful insights and make predictions.
Consider a sociological study on income distribution in a particular city. The bell curve can be used to visualize the distribution of incomes, with the mean representing the typical income level. This distribution can reveal income disparities, identify socioeconomic groups, and inform policy decisions aimed at reducing inequality.
The Art of Creating a Perfect Bell Curve
While the bell curve often occurs naturally in many scenarios, there are instances where it needs to be constructed or approximated. Creating a perfect bell curve requires careful consideration of the data and its underlying characteristics.
Data Collection and Sampling
The first step in creating a bell curve is to collect and analyze the relevant data. This involves careful sampling techniques to ensure that the data is representative of the population or phenomenon being studied. The sample size and the method of data collection play a crucial role in obtaining an accurate and reliable distribution.
For instance, in a medical study, researchers might collect data on the height of a large sample of individuals. By carefully selecting a diverse and representative sample, they can ensure that the resulting bell curve accurately reflects the height distribution in the general population.
Data Transformation and Standardization
In some cases, the raw data might not follow a perfect bell curve distribution. Transformations and standardization techniques can be applied to transform the data into a normal distribution. This process involves adjusting the scale, shifting the mean, or applying mathematical transformations to align the data with the bell curve’s characteristics.
Consider a dataset of exam scores, where the distribution is skewed towards higher scores. By applying a logarithmic transformation, the skewed distribution can be transformed into a more symmetric and bell-shaped curve, making it easier to analyze and interpret.
Parameter Estimation
Once the data has been collected and transformed, the next step is to estimate the parameters of the bell curve, namely the mean and standard deviation. These parameters define the position and shape of the curve and are crucial for accurate predictions and interpretations.
In a statistical software, the parameters can be estimated using various methods, such as maximum likelihood estimation or moment-based estimators. These techniques ensure that the estimated parameters are unbiased and provide a good fit to the observed data.
Limitations and Extensions of the Bell Curve
While the bell curve is a powerful and versatile tool, it is not without its limitations. In certain scenarios, the distribution of data might deviate significantly from the bell curve, indicating the presence of other underlying patterns or distributions.
Skewed and Non-Normal Distributions
In some cases, the data might exhibit a skewed distribution, where the majority of data points are concentrated on one side of the mean. This can occur when there are external influences or underlying factors that affect the data in a non-symmetric manner. In such cases, the bell curve might not provide an accurate representation.
For example, in a study of income distribution, the data might show a skewed distribution, with a long tail on the right side, indicating the presence of a small number of extremely high-income earners. The bell curve would not adequately capture this distribution, and alternative distributions, such as the log-normal distribution, might be more appropriate.
Multimodal Distributions
In other scenarios, the data might exhibit a multimodal distribution, where there are multiple peaks or modes in the distribution. This can occur when there are distinct subgroups or categories within the data, each with its own characteristic distribution.
Consider a study on the distribution of body mass index (BMI) in a population. The data might show a bimodal distribution, with one peak representing individuals with a healthy BMI and another peak representing individuals with an overweight or obese BMI. The bell curve would not capture this complex distribution, and alternative methods, such as mixture models, would be more suitable.
Extensions and Alternative Distributions
To address the limitations of the bell curve, statisticians and researchers have developed a wide range of alternative distributions and models. These extensions allow for more flexibility and accuracy in modeling real-world phenomena.
- The Student's t-distribution is often used when the sample size is small or the population variance is unknown.
- The chi-squared distribution is used in hypothesis testing and goodness-of-fit analyses.
- The F-distribution is employed in the analysis of variance (ANOVA) and comparing variances between groups.
- The log-normal distribution is suitable for modeling skewed data, such as income or financial returns.
- The gamma distribution is used in reliability analysis and modeling waiting times.
The Future of the Bell Curve and Its Impact

As our understanding of statistics and data analysis continues to evolve, the bell curve remains a fundamental concept with far-reaching implications. Its simplicity and versatility make it a cornerstone of many fields, from physics to finance, and its applications are only limited by our imagination.
Advancements in Statistical Modeling
With the advancement of computational power and statistical techniques, the bell curve and its extensions have become even more powerful tools. Advanced algorithms and machine learning techniques allow for more accurate estimation of parameters and more flexible modeling of complex distributions.
For example, in the field of machine learning, the bell curve is used in various algorithms, such as Gaussian mixture models and kernel density estimation, to model and classify data. These techniques enable the development of intelligent systems that can learn and adapt to complex patterns in data.
Data-Driven Decision Making
In today’s data-driven world, the bell curve plays a crucial role in informing decision-making processes. By analyzing and interpreting data through the lens of the bell curve, organizations and individuals can make informed choices, optimize processes, and achieve their goals.
Consider a business that wants to optimize its pricing strategy. By analyzing the distribution of customer preferences and willingness to pay, the bell curve can help identify the ideal price point that maximizes revenue and customer satisfaction. This data-driven approach allows businesses to make strategic decisions based on empirical evidence.
Social and Economic Impact
The bell curve’s impact extends beyond the realm of statistics and into the social and economic fabric of our society. It has shaped our understanding of equality, fairness, and justice, influencing policies and decisions at all levels.
For instance, in education, the bell curve is used to set standards and benchmarks, ensuring that students are assessed fairly and consistently. It helps identify areas where additional support or resources are needed, promoting equality of opportunity. Similarly, in healthcare, the bell curve is used to analyze the distribution of disease prevalence, guiding resource allocation and policy decisions.
Conclusion: Embracing the Beauty of the Bell Curve
The bell curve, with its elegant symmetry and profound insights, is a true marvel of mathematical beauty. Its applications are vast and diverse, and its impact on our understanding of the world is immeasurable. As we continue to explore and uncover the secrets of the perfect bell curve, we unlock new possibilities and avenues for growth and discovery.
Whether it is in the classroom, the factory floor, the stock market, or the social sciences, the bell curve remains a guiding light, illuminating the path towards understanding and progress. By embracing the beauty and power of the bell curve, we can make informed decisions, solve complex problems, and shape a better future.
How is the bell curve used in quality control?
+The bell curve is used in quality control to assess the distribution of product characteristics and identify defects or inconsistencies. By analyzing the data, manufacturers can optimize their processes and ensure consistent quality.
What are the limitations of the bell curve in data analysis?
+The bell curve has limitations when dealing with skewed or multimodal distributions. In such cases, alternative distributions and models, such as the log-normal or mixture models, might be more appropriate.
How does the bell curve impact social and economic policies?
+The bell curve has shaped our understanding of fairness and equality, influencing policies and decisions in education, healthcare, and other social domains. It helps identify areas where resources and support are needed, promoting social justice and equality of opportunity.



