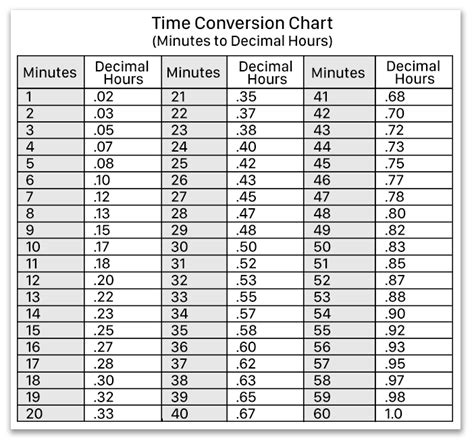
5 Tips: Corresponding Angles Theorem

Unraveling the Mysteries of Corresponding Angles

In the realm of geometry, where lines intersect and shapes intertwine, the Corresponding Angles Theorem emerges as a cornerstone principle. This theorem, a fundamental concept in mathematics, provides us with a powerful tool to understand and analyze the relationships between angles formed by intersecting lines.

The Theorem in a Nutshell

The Corresponding Angles Theorem states that when two lines are cut by a transversal, the corresponding angles formed at the intersection are congruent. In simpler terms, if you have two lines, let's call them Line A and Line B, and they are intersected by a third line, known as the transversal, the angles that are in the same position relative to the transversal are equal in measure.

Visualizing the Theorem

Let's illustrate this with a simple diagram. Consider two lines, Line A and Line B, intersected by a transversal. We'll label the corresponding angles as A, B, C, and D.

According to the Corresponding Angles Theorem, angles A and C are corresponding angles, and angles B and D are also corresponding. This means that A and C have the same measure, and B and D are congruent as well.

5 Practical Tips to Master the Theorem

1. Understand the Terminology

   Familiarize yourself with the key terms: transversal, corresponding angles, and congruent angles. These terms are the building blocks of the theorem.

2. Practice with Real-World Examples

   Apply the theorem to everyday scenarios. For instance, consider road intersections or architectural designs. Look for lines and angles, and identify corresponding angles to reinforce your understanding.

3. Explore Different Transversal Positions

   Investigate how the position of the transversal affects the corresponding angles. Move the transversal closer to or further away from the intersecting lines to observe the angle changes.

4. Use Visual Aids and Diagrams

   Visual representations are powerful tools. Create your own diagrams or refer to existing ones to solidify your understanding of the theorem. Visualizing the angles and their relationships will make it easier to grasp.

5. Apply to Geometric Problems

   The Corresponding Angles Theorem is not just a theoretical concept. Use it to solve geometric problems involving angles and intersecting lines. Practice makes perfect, and applying the theorem in practical scenarios will enhance your skills.

FAQs

<div class="faq-item">
  <div class="faq-question">
    <h3>Can corresponding angles ever be different in measure?</h3>
    <span class="faq-toggle">+</span>
  </div>
  <div class="faq-answer">
    <p>No, corresponding angles are always congruent, meaning they have the same measure. This is a fundamental principle of the Corresponding Angles Theorem.</p>
  </div>
</div>

<div class="faq-item">
  <div class="faq-question">
    <h3>How does the theorem apply to real-world scenarios?</h3>
    <span class="faq-toggle">+</span>
  </div>
  <div class="faq-answer">
    <p>The theorem is applicable in various real-world situations, such as understanding road intersections, architectural designs, and even in engineering and physics. It helps us analyze and predict the relationships between angles in practical contexts.</p>
  </div>
</div>

<div class="faq-item">
  <div class="faq-question">
    <h3>Are there any limitations to the Corresponding Angles Theorem?</h3>
    <span class="faq-toggle">+</span>
  </div>
  <div class="faq-answer">
    <p>The theorem assumes that the lines are straight and intersect at a single point. Curved lines or multiple intersections may require additional geometric principles for analysis.</p>
  </div>
</div>

<div class="faq-item">
  <div class="faq-question">
    <h3>How can I improve my understanding of corresponding angles?</h3>
    <span class="faq-toggle">+</span>
  </div>
  <div class="faq-answer">
    <p>Practice is key. Work through a variety of problems, create your own diagrams, and apply the theorem to real-world scenarios. The more you engage with the concept, the deeper your understanding will become.</p>
  </div>
</div>