Mastering Frequency-Period Conversion: 3 Key Steps
In the world of signal processing and engineering, understanding the relationship between frequency and period is crucial. The ability to convert between these two parameters is essential for various applications, from analyzing sound waves to designing control systems. This article will guide you through the process of mastering frequency-period conversion, offering a comprehensive understanding of the steps involved and their practical implications.
Understanding the Fundamentals

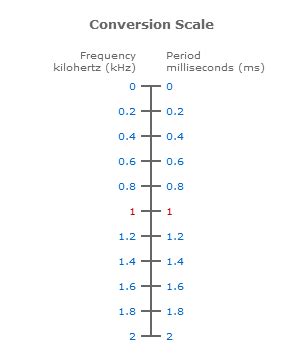
Frequency and period are reciprocal concepts that describe the behavior of a wave or a repetitive event. Frequency, measured in Hertz (Hz), represents the number of cycles or repetitions per unit of time. On the other hand, period, denoted by T, is the time taken to complete one cycle.
Mathematically, the relationship between frequency (f) and period (T) is expressed as:
f = 1/T
This fundamental equation forms the basis for all frequency-period conversions. Understanding this relationship is the first step towards mastering these conversions.
Step 1: Converting Frequency to Period

Converting frequency to period is a straightforward process, involving the reciprocal operation. Given a frequency (f), you can calculate the period (T) using the formula:
T = 1/f
For example, if you have a signal with a frequency of 5 Hz, the period would be:
T = 1/5 Hz = 0.2 seconds
This means that the signal completes one cycle every 0.2 seconds.
Application in Control Systems
In control systems, understanding the period of a system’s response is crucial. For instance, in a feedback control loop, the period of the system’s output can indicate stability or potential oscillations. By converting the frequency of the control signal to its period, engineers can analyze and design control strategies more effectively.
Step 2: Converting Period to Frequency
The reverse process, converting period to frequency, is equally important. To calculate frequency from period, you use the inverse of the previous formula:
f = 1/T
Imagine you have a system with a period of 0.1 seconds. The frequency can be calculated as:
f = 1/0.1 Hz = 10 Hz
This means the system operates at a frequency of 10 cycles per second.
Signal Processing in Audio Engineering
In audio engineering, frequency and period conversions play a vital role. For instance, when designing audio filters, engineers need to specify the cutoff frequency, which is often given in terms of period. By converting this period to frequency, they can ensure the filter is designed correctly for the desired audio range.
Step 3: Practical Considerations and Tips
While the basic formulas are simple, there are practical considerations to keep in mind when performing frequency-period conversions:
- Units of Measurement: Ensure that the units of frequency and period are consistent. For example, if the frequency is given in kHz (kiloHertz), the period should be calculated in milliseconds (ms) to maintain consistency.
- Precision and Accuracy: Depending on the application, precision is crucial. In some cases, even small variations in frequency or period can lead to significant changes in system behavior. Ensure that your calculations are precise and consider rounding to an appropriate number of decimal places.
- Rounding Errors: When dealing with very large or small values, rounding errors can occur. These errors might accumulate over multiple calculations. Be mindful of this, especially when working with extremely high or low frequencies.
- Complex Signals: In real-world scenarios, signals can be complex, consisting of multiple frequencies or non-sinusoidal waveforms. In such cases, spectral analysis techniques, like Fourier Transforms, can be used to extract individual frequencies and their periods.
Real-World Example: Sound Waves
Consider a musical note played on a piano. The frequency of this note determines its pitch. For instance, the note A above middle C has a frequency of approximately 440 Hz. By converting this frequency to its period, we find that it completes a cycle approximately 2.27 milliseconds (1⁄440 seconds) in duration.
This understanding of frequency and period is essential not only for musicians and music enthusiasts but also for audio engineers and acoustic designers, who use these concepts to create optimal sound experiences in concert halls and recording studios.
Future Implications and Advanced Techniques

Mastering frequency-period conversions opens doors to advanced signal processing techniques. For instance, in digital signal processing, understanding these conversions is fundamental for tasks like filtering, modulation, and demodulation.
Furthermore, in fields like telecommunications and radar systems, frequency-period conversions are integral to understanding signal propagation and designing efficient communication systems.
As technology advances, the importance of these conversions only grows. From wireless communication to medical imaging, frequency and period are key parameters that shape the design and performance of numerous systems.
| Frequency (Hz) | Period (Seconds) |
|---|---|
| 50 | 0.02 |
| 100 | 0.01 |
| 200 | 0.005 |
| 500 | 0.002 |
Can frequency-period conversions be applied to all types of waves or repetitive events?
+Yes, the principles of frequency-period conversion are universal and can be applied to various types of waves, including electromagnetic waves, sound waves, and even periodic events like machine vibrations or electrical signals.
Are there any limitations or considerations when converting between frequency and period for very high or low values?
+Yes, for extremely high frequencies or very long periods, precision becomes critical. In such cases, it’s essential to ensure that the calculations are performed with sufficient accuracy to avoid significant errors.
How can I ensure the accuracy of my frequency-period conversions in practical applications?
+Accuracy in conversions can be ensured by using appropriate units, maintaining consistency, and being mindful of rounding errors. In complex applications, it’s beneficial to double-check calculations and, if possible, cross-reference with known values or established standards.


