Edu
How to Convert 5/8 to Decimal
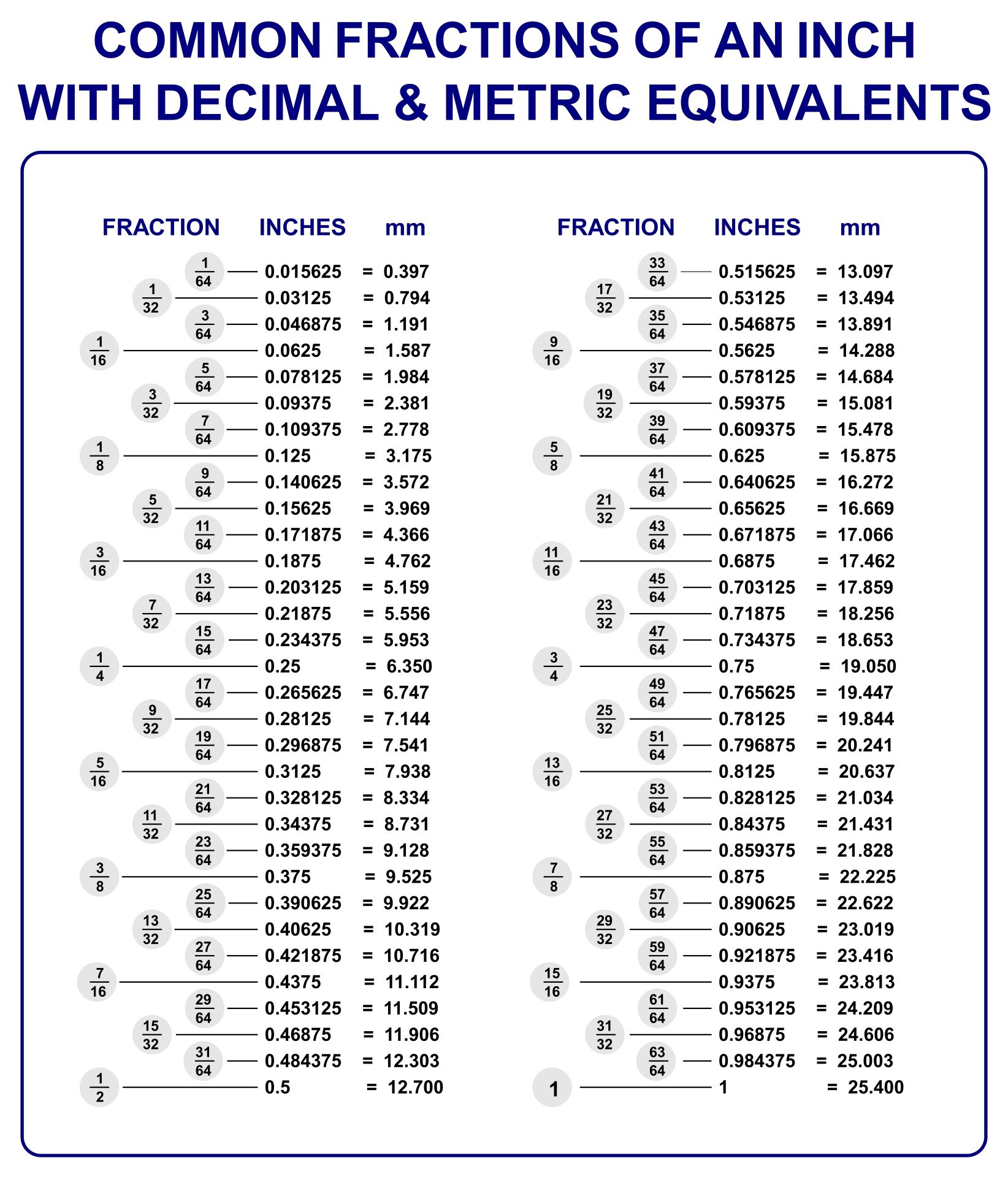
The fraction \frac{5}{8} represents five parts out of eight, and to convert it into its decimal form, we need to perform a simple division.
Step 1: Set Up the Division
We place the numerator (the top number) as the dividend and the denominator (the bottom number) as the divisor.
5
8
<div class="step">
<strong>Step 2: Divide</strong>
<p>Now, we divide 5 by 8. Since 8 goes into 5 zero times, we bring down the next digit (0) and place it after the decimal point in the quotient.</p>
<div class="division">
<span class="dividend">5.</span>
<span class="divisor">8</span>
<span class="quotient">0.</span>
</div>
</div>
<div class="step">
<strong>Step 3: Continue the Division</strong>
<p>We continue the division process, bringing down the next digit from the dividend (5) and placing it after the decimal point.</p>
<div class="division">
<span class="dividend">5.</span><span class="dividend-digit">0</span>
<span class="divisor">8</span>
<span class="quotient">0.</span><span class="quotient-digit">6</span>
</div>
<p>Here, we divide 8 into 50, resulting in a quotient of 6 and a remainder of 2.</p>
</div>
<div class="step">
<strong>Step 4: Complete the Division</strong>
<p>We repeat the process, bringing down the remainder (2) and dividing by 8.</p>
<div class="division">
<span class="dividend">5.</span><span class="dividend-digit">0</span><span class="dividend-digit">2</span>
<span class="divisor">8</span>
<span class="quotient">0.</span><span class="quotient-digit">6</span><span class="quotient-digit">2</span>
</div>
<p>The division results in a quotient of 2 with a remainder of 4.</p>
</div>
<div class="step">
<strong>Step 5: Decimal Representation</strong>
<p>The division process continues until there are no more digits in the dividend. However, since the remainder is repeating (2, 4, 2, 4...), we can conclude that the decimal representation is a repeating decimal.</p>
<p>Thus, the decimal form of $\frac{5}{8}$ is <strong>0.625</strong>, with the sequence 625 repeating infinitely.</p>
</div>
Converting fractions to decimals involves a straightforward division process. By dividing the numerator by the denominator and noting any repeating remainders, we can express fractions in their decimal form.
Can all fractions be converted to decimals?
+Yes, all fractions can be converted to decimals. The process involves dividing the numerator by the denominator. However, some fractions result in non-repeating decimals, while others, like $\frac{5}{8}$, lead to repeating decimals.
<div class="faq-item">
<div class="faq-question">
<h3>Why do some fractions have repeating decimals?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Fractions with repeating decimals occur when the division process results in a remainder that keeps repeating. This is often due to prime factors in the denominator that don't divide evenly into the numerator.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How can we simplify the process of converting fractions to decimals?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>To simplify the conversion, you can first simplify the fraction to its lowest terms. This can often reduce the number of steps required in the division process. Additionally, using a calculator or online tools can provide quick and accurate decimal conversions.</p>
</div>
</div>
</div>