Un viaje a la estadística: conceptos esenciales
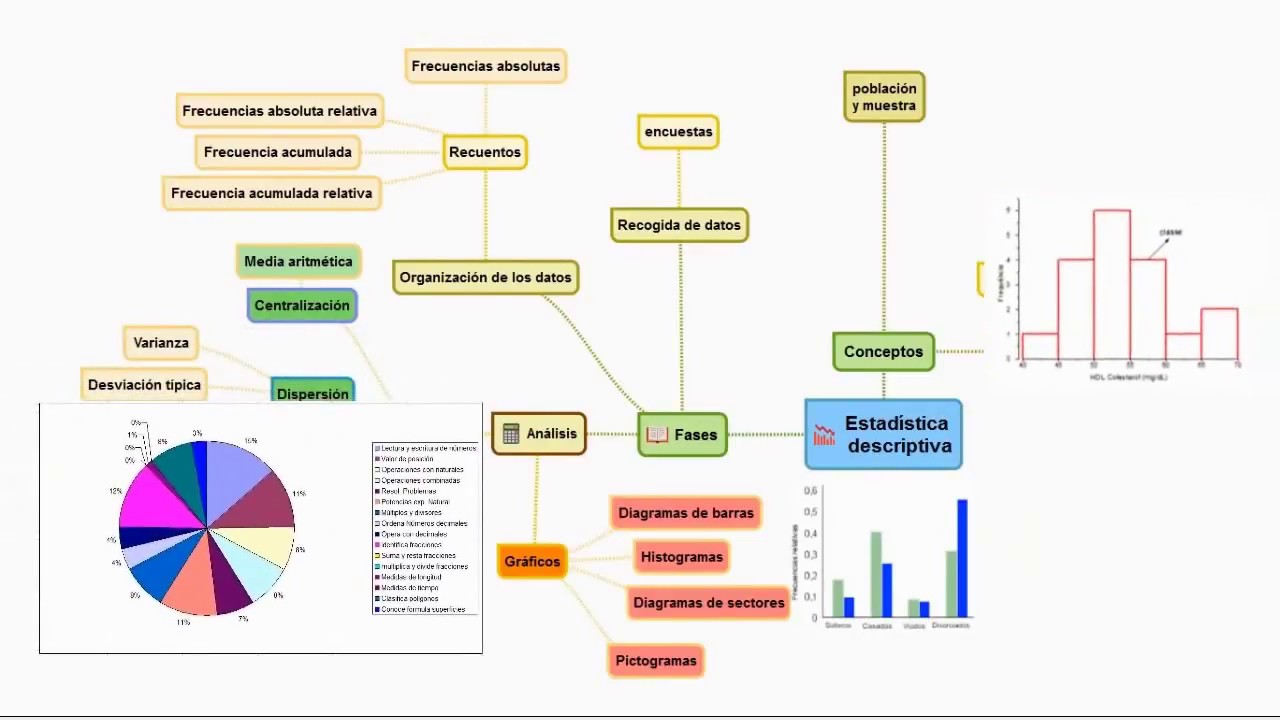
La estadística es una herramienta poderosa que nos permite comprender y analizar grandes cantidades de datos, brindándonos valiosas perspectivas e insights. En este artículo, exploraremos los conceptos esenciales de la estadística, desde sus fundamentos hasta su aplicación en el mundo real, para ayudarte a profundizar en este fascinante campo de estudio.
La importancia de la estadística en la toma de decisiones
En un mundo inundado de información, la estadística desempeña un papel crucial en la toma de decisiones informadas. Ya sea en la investigación científica, la economía, la salud pública o cualquier otro campo, la capacidad de interpretar y analizar datos es esencial para tomar decisiones basadas en evidencia. La estadística nos permite extraer patrones, identificar tendencias y predecir resultados, proporcionando una base sólida para la toma de decisiones estratégicas.
Por ejemplo, imagina que una empresa farmacéutica desea determinar la efectividad de un nuevo medicamento. A través del análisis estadístico, pueden evaluar los datos de ensayos clínicos, comparar grupos de control y tratamiento, y calcular medidas como la significancia estadística. Estos análisis guían a los investigadores en la toma de decisiones críticas, asegurando que los medicamentos sean seguros y efectivos antes de su lanzamiento al mercado.
Fundamentos de la estadística descriptiva

La estadística descriptiva se enfoca en resumir y describir conjuntos de datos. Esta rama de la estadística nos permite comprender las características de una población o muestra mediante el uso de medidas de tendencia central, dispersión y gráficos.
Medidas de tendencia central
Las medidas de tendencia central, como la media, la mediana y la moda, nos ayudan a identificar el valor típico de un conjunto de datos. Por ejemplo, si deseamos describir la altura promedio de una población, utilizaríamos la media como medida de tendencia central.
| Medida | Definición |
|---|---|
| Media | El promedio de los valores de un conjunto de datos. |
| Mediana | El valor que divide a los datos en dos partes iguales. |
| Moda | El valor que aparece con mayor frecuencia. |

Medidas de dispersión
Las medidas de dispersión, como la desviación estándar y el rango intercuartílico, nos permiten evaluar la variabilidad de los datos. Estas medidas nos indican cuán dispersos están los valores en comparación con la medida de tendencia central.
| Medida | Definición |
|---|---|
| Desviación estándar | Mide la cantidad de dispersión de los datos alrededor de la media. |
| Rango intercuartílico | La diferencia entre el percentil 75 y el percentil 25, excluyendo los valores extremos. |
Gráficos estadísticos
Los gráficos estadísticos, como histogramas, diagramas de caja y gráficos de dispersión, son herramientas visuales poderosas que nos permiten visualizar y comprender mejor los datos. Estos gráficos nos ayudan a identificar patrones, distribuciones y relaciones entre variables.
Introducción a la estadística inferencial
La estadística inferencial nos permite realizar inferencias y generalizaciones a partir de muestras de datos, para hacer afirmaciones sobre una población más grande. Esta rama de la estadística es crucial en la investigación científica y en la toma de decisiones en diversas áreas.
Estimación de parámetros
En estadística inferencial, estimamos parámetros desconocidos de una población a partir de muestras. Por ejemplo, podemos utilizar una muestra de estudiantes para estimar la proporción de la población estudiantil que aprueba un examen.
Pruebas de hipótesis
Las pruebas de hipótesis nos permiten evaluar si una afirmación o hipótesis sobre una población es verdadera o falsa. Estas pruebas se basan en el análisis de muestras y en la comparación de resultados estadísticos con una distribución teórica.
Intervalos de confianza
Los intervalos de confianza son una herramienta importante en la estadística inferencial. Nos permiten estimar un rango de valores en el que es probable que se encuentre un parámetro desconocido, con un nivel de confianza determinado. Por ejemplo, podemos calcular un intervalo de confianza para la media de una población, indicando que, con un 95% de confianza, la media verdadera se encuentra dentro de ese intervalo.
Análisis de regresión y correlación
El análisis de regresión y correlación es una herramienta estadística poderosa para comprender la relación entre variables. Nos permite modelar y predecir valores de una variable en función de otras variables.
Correlación
La correlación mide la fuerza y dirección de la relación lineal entre dos variables. Puede ser positiva (aumento en una variable corresponde con aumento en la otra), negativa (aumento en una variable corresponde con disminución en la otra) o nula (no hay relación).
Análisis de regresión lineal
El análisis de regresión lineal nos permite establecer una relación lineal entre una variable dependiente y una o más variables independientes. A través de modelos de regresión, podemos predecir valores de la variable dependiente a partir de los valores de las variables independientes.
Ejemplo: Predicción de precios de viviendas
Supongamos que queremos predecir el precio de una vivienda en función de su tamaño (en metros cuadrados) y su ubicación (distancias en kilómetros a centros comerciales, escuelas, etc.). Podríamos utilizar un modelo de regresión lineal múltiple para estimar el precio en función de estas variables. A través del análisis de regresión, podemos determinar la importancia relativa de cada variable en la predicción y obtener una ecuación que nos permita predecir precios de viviendas en el futuro.
Análisis de varianza (ANOVA)

El análisis de varianza (ANOVA) es una técnica estadística utilizada para comparar la media de dos o más grupos de datos. Nos permite evaluar si hay diferencias significativas entre las medias de estos grupos.
Tipos de ANOVA
- ANOVA de un factor: Compara la media de dos o más grupos que difieren en un solo factor.
- ANOVA de dos factores: Compara la media de grupos que difieren en dos factores.
- ANOVA de diseño factorial: Permite estudiar la interacción entre múltiples factores.
Aplicación: Estudio de la eficacia de tratamientos médicos
En un estudio clínico, se quiere evaluar la eficacia de tres tratamientos diferentes para una enfermedad. Se asigna aleatoriamente a pacientes en tres grupos y se mide la respuesta al tratamiento. A través del ANOVA, se puede determinar si existe una diferencia significativa en la respuesta al tratamiento entre los tres grupos, lo que podría guiar decisiones clínicas futuras.
Conclusión: El poder de la estadística
La estadística es una herramienta esencial en la era de la información. Nos permite extraer información valiosa de grandes conjuntos de datos, guiar decisiones estratégicas y comprender mejor el mundo que nos rodea. Desde la descripción de datos hasta la inferencia y la predicción, la estadística ofrece un marco robusto para la investigación y la toma de decisiones basadas en evidencia.
En este artículo, hemos explorado los conceptos fundamentales de la estadística, desde la estadística descriptiva hasta la inferencial, pasando por la correlación y el análisis de varianza. Estos conceptos son la base para una comprensión más profunda de la disciplina y su aplicación en diversas áreas. La estadística es una herramienta poderosa que sigue evolucionando y adaptándose a las necesidades de una sociedad cada vez más orientada a los datos.
¿Cómo se utilizan las medidas de tendencia central en la toma de decisiones empresariales?
+Las medidas de tendencia central, como la media, la mediana y la moda, son herramientas valiosas en la toma de decisiones empresariales. Por ejemplo, una empresa puede utilizar la media para determinar el salario promedio de sus empleados, lo que ayuda a tomar decisiones sobre compensaciones y beneficios. La mediana puede ser útil para identificar la posición central en distribuciones salariales asimétricas, mientras que la moda puede ser relevante en la identificación de valores típicos o populares.
¿Cuál es la diferencia entre un diagrama de caja y un histograma?
+Un diagrama de caja (o caja y bigotes) es un gráfico que muestra la distribución de datos a través de sus cuartiles, incluyendo la mediana y los valores extremos. Es útil para visualizar la forma y simetría de una distribución. Por otro lado, un histograma es un gráfico de barras que muestra la frecuencia de aparición de valores en rangos específicos. Los histogramas son útiles para identificar patrones y distribuciones de datos.
¿Cómo se elige el nivel de confianza en un intervalo de confianza?
+El nivel de confianza en un intervalo de confianza se elige en función de la certeza que se desea tener en la estimación del parámetro desconocido. El nivel de confianza más común es el 95%, lo que significa que se espera que el intervalo de confianza contenga el verdadero valor del parámetro en el 95% de los casos. Sin embargo, se pueden elegir otros niveles de confianza, como el 90% o el 99%, dependiendo de la situación y los requerimientos específicos.



