Mastering Capacitor Charging: 3 Key Equations
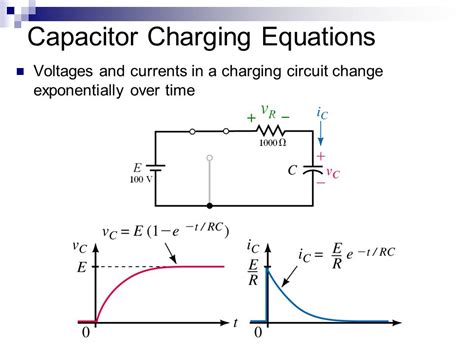
The world of electronics is filled with intricate processes, and one fundamental aspect revolves around capacitor charging. This process is integral to various applications, from simple circuits to complex power systems. To truly understand and master capacitor charging, it’s crucial to delve into the underlying mathematical principles. Here, we present three key equations that are essential for anyone seeking to grasp this topic.
- Capacitor Charging Formula The first equation is the fundamental capacitor charging formula, which describes how the voltage across a capacitor changes over time when a constant current is applied:
$ V(t) = V_0(1 - e^{-t/\tau}) $
In this equation: - V(t) represents the voltage across the capacitor at time t. - V_0 is the initial voltage across the capacitor. - e is the base of the natural logarithm. - t is the time in seconds. - \tau is the time constant, which is determined by the capacitance C and the resistance R in the circuit (\tau = RC).
This equation illustrates how the voltage across the capacitor approaches the source voltage (V_0) over time, with the rate of charging dependent on the time constant \tau.
- Time Constant and Circuit Behavior The second equation delves into the concept of the time constant and its impact on circuit behavior:
$ \tau = RC $
Here, R represents the resistance in the circuit (ohms, \Omega), and C is the capacitance (farads, F). This equation showcases how the time constant, \tau, is directly proportional to the product of resistance and capacitance.
Understanding the time constant is crucial as it dictates the speed at which the capacitor charges or discharges. A larger time constant indicates a slower charging process, while a smaller time constant results in faster charging.
- Energy Stored in a Capacitor The third equation focuses on the energy stored within a charged capacitor:
$ E = \frac{1}{2}CV^2 $
In this equation: - E is the energy stored in the capacitor (joules, J). - C is the capacitance (farads, F). - V is the voltage across the capacitor (volts, V).
This equation highlights the relationship between capacitance, voltage, and the energy stored in the capacitor. As the capacitance or voltage increases, so does the energy stored, emphasizing the importance of these factors in capacitor-based energy storage systems.
Mastering these equations is essential for anyone working with capacitor-based circuits, as they provide the foundation for understanding and predicting the behavior of these systems. From designing efficient power supplies to optimizing energy storage systems, a deep understanding of these mathematical principles is key.
Now, let’s delve into some practical examples and explore how these equations manifest in real-world scenarios, ensuring a comprehensive grasp of capacitor charging dynamics.



