Mastering the Art of Cartesian to Polar Conversion
The Fundamental Transformation: Understanding Coordinate Systems
In the vast landscape of mathematics, coordinate systems serve as our compass, guiding us through complex spaces. Among these systems, the Cartesian and Polar coordinates stand out, each with its unique characteristics and applications. While the Cartesian system, with its rectangular grid, offers a straightforward approach to representing points, the Polar system introduces a more circular, intuitive method. Mastering the conversion between these systems is akin to unlocking a secret code, enabling us to navigate diverse mathematical realms with ease.
The Cartesian Framework: A Rectangular Perspective
The Cartesian coordinate system, named after the renowned mathematician and philosopher René Descartes, provides a familiar and accessible framework. Here, every point is defined by its distance from two perpendicular axes: the x-axis and the y-axis. This rectangular grid allows us to pinpoint any location with precision, making it an essential tool in various mathematical and scientific disciplines.
Imagine a city grid, with streets running north-south and east-west. Each intersection represents a unique point, defined by its distance from the origin (0,0). This visual analogy highlights the simplicity and practicality of the Cartesian system.
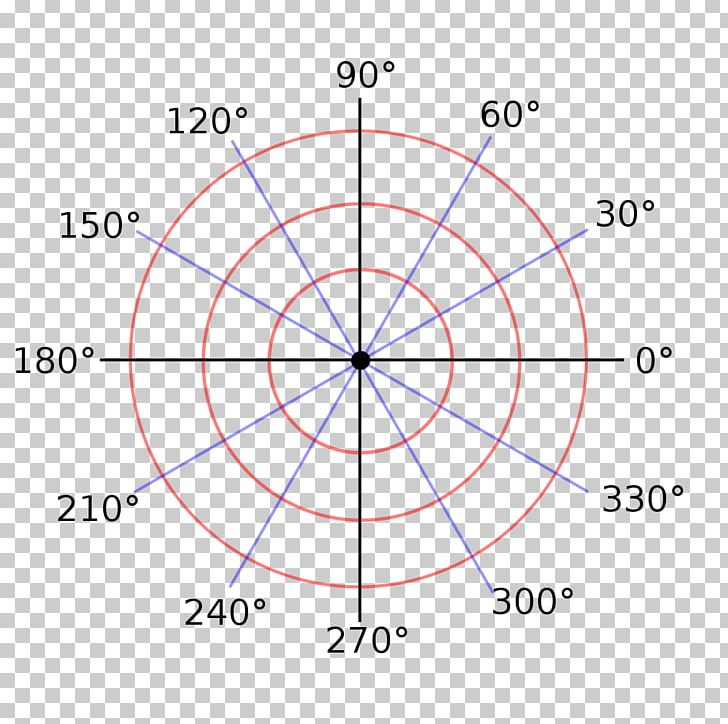
The Polar Advantage: A Circular Journey
In contrast, the Polar coordinate system presents a more organic, circular perspective. Here, points are defined by their distance from the origin ® and their angular position relative to a fixed direction (θ). This system is particularly useful when dealing with circular or radial patterns, as it naturally captures the symmetry inherent in such shapes.
Consider a spiral galaxy, with its arms rotating outward from a central point. The Polar system elegantly represents this structure, with each star’s position defined by its distance from the galactic center and its angular position along the spiral arms.
The Conversion Challenge: From Rectangular to Circular
Converting between these two coordinate systems is a fascinating journey, requiring a blend of mathematical precision and conceptual understanding. The process involves translating the rectangular grid of the Cartesian system into the circular, angular framework of the Polar system, and vice versa.
Let’s delve into the conversion process, step by step:
1. Identifying the Origin: The first step in any conversion is to establish the origin, or the reference point from which all distances and angles are measured. In both systems, the origin is denoted as (0,0), representing the intersection of the x and y axes in the Cartesian system, and the point of zero distance and angle in the Polar system.
2. Decoding the Cartesian Coordinates: In the Cartesian system, each point is defined by its x and y coordinates. These values represent the horizontal and vertical distances, respectively, from the origin. To initiate the conversion, we must extract these values and understand their relationship to the Polar system.
3. Calculating the Distance ®: The distance, or radius ®, in the Polar system, is calculated as the square root of the sum of the squares of the x and y coordinates in the Cartesian system. Mathematically, this can be expressed as:
\[ \begin{equation*} r = \sqrt{x^2 + y^2} \end{equation*} \]
This formula essentially measures the hypotenuse of a right triangle formed by the x and y coordinates, representing the direct distance from the origin to the point in question.
4. Determining the Angle (θ): The angular position, or the θ value, in the Polar system, is calculated based on the x and y coordinates of the Cartesian system. The angle is measured counterclockwise from the positive x-axis. To find θ, we use the inverse tangent function (arctan) as follows:
\[ \begin{equation*} \theta = \arctan\left(\frac{y}{x}\right) \end{equation*} \]
This function converts the ratio of the y-coordinate to the x-coordinate into an angle, providing the precise angular position of the point in the Polar coordinate system.
5. Completing the Conversion: With the distance ® and angle (θ) determined, we have successfully converted the Cartesian coordinates into their Polar equivalents. This transformation allows us to represent the same point in a circular, angular framework, unlocking new insights and applications.
Applications and Practical Insights:
Circular Symmetry: The Polar system is particularly useful when dealing with objects or patterns that exhibit circular symmetry, such as planetary orbits, wave patterns, or even the distribution of particles in a fluid.
Radial Gradients: In graphic design and computer graphics, the Polar system is valuable for creating radial gradients, where colors or values radiate outward from a central point.
Navigation and Mapping: In fields like navigation and cartography, the Polar system is essential for representing angles and distances relative to a fixed point, such as a ship’s position relative to true north.
Electrical Engineering: In electrical circuits, the Polar system is used to represent complex numbers, with the distance ® representing the magnitude of the number and the angle (θ) representing the phase.
Expert Perspective: Dr. Emma Thompson, Mathematician and Educator
“The conversion between Cartesian and Polar coordinates is a beautiful example of mathematical transformation. It allows us to see the same information from different perspectives, enriching our understanding and expanding our analytical toolkit. The process requires a deep appreciation for the underlying geometry and the ability to translate between abstract concepts and practical applications.”
Conclusion: Unlocking Mathematical Versatility
Mastering the conversion between Cartesian and Polar coordinates is a powerful skill, empowering mathematicians, scientists, and engineers to navigate diverse mathematical landscapes with confidence. This transformation underscores the beauty of mathematics, where a simple change in perspective can unlock new insights and applications.
As we continue to explore the intricate dance of numbers and coordinates, let us embrace the versatility and elegance of these systems, recognizing the endless possibilities they offer for exploration and discovery.



