Mastering the Black-Scholes Model in Excel
Welcome to a comprehensive guide on mastering the Black-Scholes Model, a powerful tool for options pricing and risk management. This article aims to equip you with the knowledge and skills to implement and utilize the Black-Scholes Model in Excel, a widely accessible and versatile spreadsheet software. By the end of this journey, you'll not only understand the theoretical foundations but also gain practical expertise in applying this model to real-world scenarios.
The Black-Scholes Model, developed by Fischer Black, Myron Scholes, and Robert Merton, is a cornerstone of financial engineering and derivatives pricing. It provides a framework to value European-style options, which are options that can only be exercised at the end of their life. This model has revolutionized the way financial professionals approach risk management and option pricing, offering a robust and widely accepted methodology.
Understanding the Black-Scholes Model
The Black-Scholes Model is a mathematical equation that calculates the theoretical fair value of a European-style call or put option. It is a key tool for option traders, risk managers, and financial analysts, as it provides a standardized approach to pricing options and managing risk.
The model takes into account several key variables: the current stock price, the strike price of the option, the time to maturity, the risk-free interest rate, and the volatility of the underlying asset. By inputting these variables, the model generates a price for the option, reflecting the market's expectations and the inherent risks.
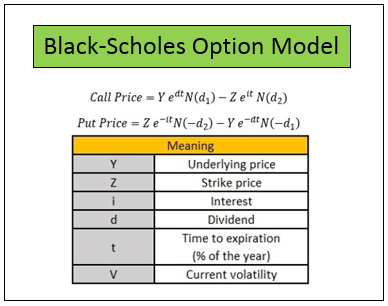
The formula for the Black-Scholes Model is as follows:
\[ \begin{equation*} C = S_0N(d_1) - Ke^{-rt}N(d_2) \end{equation*} \]
Where:
- C is the price of the call option.
- S0 is the current price of the underlying asset.
- N(d1) is the cumulative distribution function of the standard normal distribution for d1.
- K is the strike price of the option.
- e is the mathematical constant e (approximately 2.71828)
- r is the risk-free interest rate.
- t is the time to maturity (in years)
- N(d2) is the cumulative distribution function of the standard normal distribution for d2, where d2 = d1 - σ√t and σ is the volatility of the underlying asset.
Understanding the formula and its components is crucial for mastering the Black-Scholes Model. Each variable plays a specific role in determining the option price, and their accurate estimation is essential for precise valuation.
Implementing the Black-Scholes Model in Excel

Excel, with its robust spreadsheet functionality, is an ideal platform for implementing the Black-Scholes Model. It allows financial professionals to create dynamic and interactive models, making it a powerful tool for option pricing and risk management.
Step 1: Setting Up the Spreadsheet
Begin by creating a new Excel spreadsheet and organizing your data. You’ll need to input the necessary variables, such as the current stock price, strike price, time to maturity, risk-free interest rate, and volatility. Ensure that your data is accurate and up-to-date, as this is critical for precise model calibration.
Step 2: Writing the Black-Scholes Formula
Next, you’ll need to write the Black-Scholes formula in Excel. This involves using Excel’s built-in functions to calculate the cumulative distribution functions N(d1) and N(d2). Excel provides the NORMSDIST function for this purpose, which calculates the standard normal cumulative distribution function. You’ll also need to use other mathematical functions like EXP, LN, and SQRT to handle the exponential and square root operations.
Here's a step-by-step guide to writing the Black-Scholes formula in Excel:
- Calculate d1 using the formula: d1 = (ln(S0/K) + (r + 0.5 * σ2) * t) / (σ * √t)
- Calculate d2 using the formula: d2 = d1 - σ * √t
- Calculate N(d1) using the NORMSDIST function: N(d1) = NORMSDIST(d1)
- Calculate N(d2) using the NORMSDIST function: N(d2) = NORMSDIST(d2)
- Finally, calculate the call option price C using the formula: C = S0 * N(d1) - Ke-rt * N(d2)
Step 3: Testing and Calibration
Once you've written the formula, it's crucial to test and calibrate your model. Compare the calculated option prices with market prices to ensure accuracy. If there are discrepancies, adjust your input variables and recalibrate until you achieve a close match.
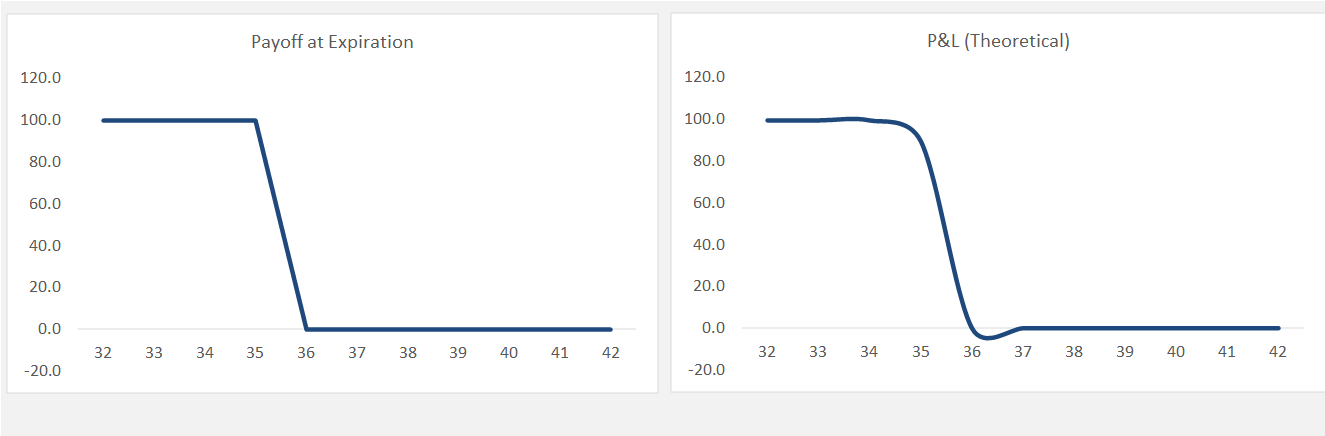
Step 4: Sensitivity Analysis
Conducting a sensitivity analysis is an important step in understanding the behavior of your model. This involves changing the input variables and observing the impact on the option price. By doing so, you can identify which variables have the most significant influence on the option price and gain insights into the model’s behavior under different market conditions.
Advanced Techniques and Real-World Applications
Mastering the Black-Scholes Model opens up a world of advanced techniques and real-world applications. Here are some key areas to explore:
Greeks and Risk Management
The Black-Scholes Model provides a foundation for understanding the Greeks, which are key risk metrics in options trading. These include Delta (sensitivity to stock price changes), Gamma (sensitivity of Delta to stock price changes), Vega (sensitivity to volatility changes), Theta (sensitivity to time decay), and Rho (sensitivity to interest rate changes). By analyzing these Greeks, financial professionals can effectively manage risk and make informed trading decisions.
Portfolio Optimization
The Black-Scholes Model can be extended to portfolio optimization, where it is used to construct optimal portfolios by considering the risk and return characteristics of various assets. By incorporating options into the portfolio, financial professionals can enhance risk-adjusted returns and improve overall portfolio performance.
Volatility Analysis
Volatility, a key input in the Black-Scholes Model, is a critical factor in options pricing. By analyzing historical volatility and market expectations, financial professionals can make more accurate predictions and improve their option pricing strategies. Tools like implied volatility and volatility smiles provide valuable insights into market sentiment and option pricing.
Real-World Case Studies
Exploring real-world case studies is an excellent way to deepen your understanding of the Black-Scholes Model. These case studies can illustrate how the model is applied in different scenarios, such as pricing exotic options, managing complex portfolios, or hedging against market risks. By analyzing real-world examples, you can gain practical insights and develop a more nuanced understanding of the model’s applications.
Conclusion: The Power of Excel and the Black-Scholes Model
The combination of Excel’s versatility and the Black-Scholes Model’s robust framework offers a powerful toolset for financial professionals. By mastering this model and its implementation in Excel, you gain the ability to price options accurately, manage risk effectively, and make informed trading decisions. The Black-Scholes Model, with its deep roots in financial theory, provides a solid foundation for exploring advanced techniques and real-world applications, making it an essential skill for anyone working in the world of finance.
What are the limitations of the Black-Scholes Model?
+While the Black-Scholes Model is a powerful tool, it has some limitations. It assumes a constant volatility and risk-free interest rate, which may not always hold true in real-world scenarios. Additionally, it only applies to European-style options and does not account for early exercise or dividends. These limitations highlight the importance of continuous learning and adapting to market dynamics.
How can I improve the accuracy of my Black-Scholes Model in Excel?
+To enhance the accuracy of your Black-Scholes Model, ensure that your input variables are up-to-date and reflect market conditions accurately. Regularly calibrate your model by comparing calculated option prices with market prices. Additionally, consider incorporating more advanced techniques, such as using historical volatility data or adjusting for dividends, to improve the model’s precision.
What are some common challenges when implementing the Black-Scholes Model in Excel?
+Some common challenges include ensuring the correct implementation of the formula, especially when dealing with complex scenarios. It is also crucial to have a deep understanding of the underlying assumptions and their implications. Additionally, managing large datasets and ensuring data integrity can be challenging. Regularly testing and calibrating your model can help overcome these challenges.