Unraveling the Arc Length Formula
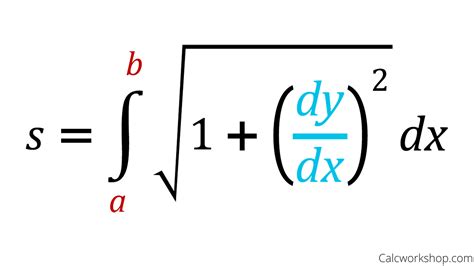
The arc length formula is a fundamental concept in mathematics, providing us with the tools to measure the distance along curved paths. This formula, though seemingly simple, has a rich history and numerous applications across various fields. Today, we delve into the intricacies of this mathematical concept, exploring its origins, its importance, and the methods by which we can derive and utilize it effectively.
At its core, the arc length formula allows us to calculate the distance covered along a curve, be it a gentle arc or a complex, winding path. This measurement is crucial in fields ranging from physics and engineering to architecture and even everyday life. Imagine navigating a winding road or tracing the path of a satellite’s orbit—the arc length formula is the key to understanding these trajectories.
Historical Evolution of the Arc Length Concept

The concept of arc length has its roots in ancient mathematics. Early civilizations, such as the Greeks and the Indians, made significant strides in understanding curved shapes and their properties. However, it was during the Renaissance period that mathematicians like Fermat and Descartes began to formalize the idea of arc length.
Fermat, in particular, made notable contributions to the field of geometry, developing methods to calculate arc lengths using infinitesimal calculus. His work laid the foundation for the modern understanding of arc length, paving the way for more sophisticated applications in the centuries to come.
The Mathematical Derivation

To grasp the arc length formula fully, we must delve into the mathematical principles that underpin it. The formula is derived from the concept of calculus, specifically the integral calculus, which deals with the accumulation of quantities.
In simple terms, the arc length of a curve is the sum of the infinitesimal lengths of all the small segments that make up the curve. This is akin to adding up an infinite number of tiny line segments to obtain the total distance. Mathematically, this can be expressed as:
\[ \begin{equation*} \text{Arc Length} = \int_{a}^{b} \sqrt{1 + (\frac{dy}{dx})^2} \, dx \, . \end{equation*} \]
Here, a and b represent the start and end points of the curve, and dx indicates the infinitesimal change in the x-coordinate. The derivative \frac{dy}{dx} represents the rate of change of the y-coordinate with respect to x.
Applications Across Disciplines
The arc length formula finds applications in a myriad of fields, each utilizing it in unique ways:
Physics: In physics, the arc length formula is crucial for understanding the paths of objects in motion. From the trajectory of a projectile to the orbit of planets, this formula helps physicists model and predict real-world phenomena.
Engineering: Engineers rely on the arc length formula to design efficient transportation systems. Whether it’s the curvature of a road, the design of a bridge, or the layout of a pipeline, the arc length formula ensures optimal designs.
Computer Graphics: In the world of computer graphics, the arc length formula is used to create smooth curves and animations. It ensures that virtual objects move along realistic and visually appealing paths.
Geography and Mapping: Cartographers and geographers use the arc length formula to accurately represent the curvature of the Earth’s surface on maps. This ensures that distances and areas are depicted accurately.
Practical Considerations and Techniques
When applying the arc length formula, several practical considerations come into play:
Curvature Complexity: Some curves are more complex than others, requiring more intricate calculations. Techniques like numerical integration or the use of specific parametric equations can help tackle these challenges.
Error Margins: Due to the nature of infinitesimal calculus, there is always a margin of error in arc length calculations. Understanding these errors and their implications is crucial for accurate results.
Software and Tools: With the advent of powerful software, calculating arc lengths has become more accessible. Tools like MATLAB, Mathematica, and specialized CAD software provide efficient ways to apply the arc length formula.
Future Trends and Emerging Applications

As technology advances, so too do the applications of the arc length formula:
Autonomous Vehicles: The precise calculation of arc lengths is vital for the development of autonomous vehicles. These vehicles must navigate complex paths with utmost accuracy, making the arc length formula a key component.
Medical Imaging: In medical imaging, the arc length formula is used to analyze and interpret curved structures like blood vessels or organs. This aids in the diagnosis and treatment of various medical conditions.
Environmental Science: Environmental scientists use the arc length formula to model and predict the paths of natural phenomena like hurricanes or the spread of pollutants.
Conclusion: A Universal Mathematical Tool
In conclusion, the arc length formula is a versatile and powerful mathematical tool with a rich history and a vast array of applications. From its ancient origins to its modern-day uses, this formula continues to play a pivotal role in our understanding of the world around us. As we continue to explore and innovate, the arc length formula will undoubtedly remain a fundamental concept, shaping our knowledge and guiding our discoveries.


