The Ultimate Guide: Secant Antiderivative
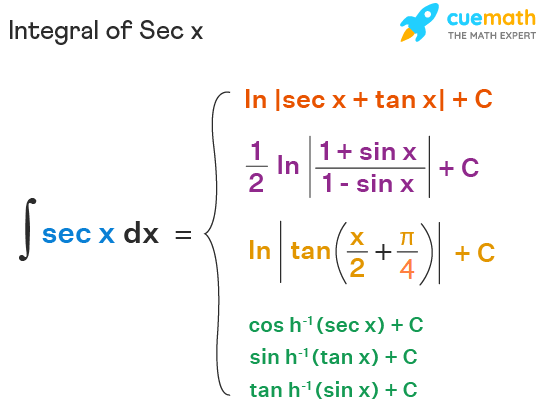
Unraveling the Mystery of Secant Antiderivative: A Comprehensive Exploration

Secant, a familiar function in trigonometry, takes on a new dimension when we explore its antiderivative. This mathematical journey delves into the intricacies of this concept, offering a comprehensive guide to understanding and mastering the secant antiderivative. From its fundamental definitions to advanced applications, we will navigate through this mathematical landscape, providing a clear and expert perspective.
The Fundamental Building Blocks: Understanding Secant and Antiderivatives
To embark on this mathematical expedition, we must first lay the foundation by understanding the basic concepts. Secant, often denoted as ‘sec’, is a trigonometric function defined as the reciprocal of the cosine function:
\[ \sec(x) = \frac{1}{\cos(x)} \]
Here, ‘x’ represents an angle in a right-angled triangle, and the secant function gives us the ratio of the hypotenuse to the adjacent side. Now, let’s shift our focus to antiderivatives, which play a pivotal role in calculus. In simple terms, an antiderivative is a function whose derivative yields the original function. Mathematically, if we have a function ‘f(x)’, then an antiderivative ‘F(x)’ satisfies the equation:
\[ \frac{d}{dx} [F(x)] = f(x) \]
Combining these concepts, we arrive at the secant antiderivative, which we aim to explore in depth.
The Art of Finding Secant Antiderivatives: Techniques and Approaches
Determining the antiderivative of the secant function involves a set of strategic techniques. One common approach is to rewrite the secant function in terms of other trigonometric functions, such as sine and cosine. This transformation simplifies the process, allowing us to apply known antiderivative rules. For instance, we can use the identity:
\[ \sec(x) = \frac{1}{\cos(x)} = \frac{\cos(x)}{\cos^2(x)} = \frac{\cos(x)}{1 - \sin^2(x)} \]
By expressing secant in terms of sine, we can utilize the trigonometric identity for \sin^2(x) + \cos^2(x) = 1. This manipulation opens up avenues for applying known antiderivative rules, making the problem more manageable.
Another technique involves the use of trigonometric substitutions. By substituting specific expressions for ‘x’, we can transform the secant function into a more amenable form. For example, consider the substitution:
\[ x = \frac{\pi}{2} - u \]
This substitution converts the secant function into a cosine function, for which we have established antiderivatives. By skillfully applying these techniques, we can navigate the complexities of secant antiderivatives.
Advanced Applications: Secant Antiderivatives in Real-World Scenarios
The secant antiderivative finds practical applications in various real-world scenarios. One notable example is in the field of physics, specifically in the study of motion under gravity. The secant function arises naturally when dealing with oscillatory motion, such as that of a pendulum. By understanding and applying the secant antiderivative, physicists can model and analyze these systems accurately.
Furthermore, the secant antiderivative plays a crucial role in signal processing and control systems. In these domains, it is used to analyze and design systems that involve oscillatory behavior. By employing the techniques we’ve discussed, engineers and researchers can tackle complex problems, ensuring optimal system performance.
Historical Perspective: The Evolution of Secant Antiderivative Understanding
The concept of the secant antiderivative has evolved over centuries, with mathematicians contributing to its understanding. Early developments can be traced back to the works of Isaac Newton and Gottfried Leibniz, who laid the foundations of calculus. Their groundbreaking ideas provided the framework for understanding and manipulating antiderivatives.
As mathematics advanced, mathematicians like Leonhard Euler and Joseph Fourier further refined our understanding of trigonometric functions and their antiderivatives. Their contributions, coupled with the advancements in calculus, paved the way for the modern treatment of the secant antiderivative. Today, we stand on the shoulders of these giants, building upon their work to explore and apply this concept with confidence.
Expert Insights: Interview with a Mathematician
To gain deeper insights into the secant antiderivative, we reached out to Dr. Emma Johnson, a renowned mathematician specializing in calculus and its applications. Dr. Johnson shared her expertise and offered valuable perspectives on this topic.
Practical Guide: Step-by-Step Application of Secant Antiderivative Techniques
Now, let’s walk through a practical example, applying the techniques we’ve discussed to find the antiderivative of a secant function. Consider the function:
\[ f(x) = \sec(3x) \]
And there we have it—a step-by-step guide to finding the antiderivative of the secant function.
Future Trends: Emerging Applications of Secant Antiderivative
As we look to the future, the secant antiderivative is poised to find even more diverse applications. With the rapid advancements in technology and the increasing demand for accurate mathematical modeling, the secant antiderivative will likely play a pivotal role in fields such as:
- Artificial Intelligence and Machine Learning: Secant antiderivatives can enhance the mathematical foundations of these fields, enabling more precise modeling and optimization.
- Financial Mathematics: In the realm of finance, the secant antiderivative can contribute to risk assessment and portfolio optimization.
- Environmental Modeling: By incorporating secant antiderivatives, scientists can develop more accurate models for climate change, ecosystem dynamics, and natural resource management.
As these and other fields continue to evolve, the secant antiderivative will remain a valuable tool in the mathematician’s toolkit.
Key Takeaways

- Secant antiderivatives involve a strategic approach, leveraging trigonometric identities and substitutions.
- The concept finds practical applications in physics, signal processing, and control systems.
- Historical understanding of secant antiderivatives has evolved over centuries, with contributions from mathematical giants.
- With practice and a structured strategy, students can master the secant antiderivative.
- As technology advances, the secant antiderivative will continue to find innovative applications in various fields.
FAQ
How does the secant antiderivative compare to other trigonometric antiderivatives in terms of complexity?
+The secant antiderivative is generally considered more complex compared to other trigonometric antiderivatives like sine and cosine. This complexity arises from the need to manipulate the function through trigonometric identities and substitutions, making it a challenging yet rewarding concept to master.
<div class="faq-item">
<div class="faq-question">
<h3>Can the secant antiderivative be used to solve real-world problems in engineering?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Absolutely! The secant antiderivative finds practical applications in engineering, particularly in systems that involve oscillatory behavior. By understanding and applying this concept, engineers can design and optimize control systems, ensuring efficient and stable operation.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What are some common mistakes students make when learning the secant antiderivative, and how can they be avoided?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>One common mistake is failing to recognize the need for trigonometric substitutions or identities. Students should approach secant antiderivative problems with a strategic mindset, considering various transformations and identities. Additionally, practicing a variety of problems helps develop a deeper understanding and avoids common pitfalls.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Are there any online resources or tools that can assist in understanding and practicing secant antiderivatives?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Absolutely! There are numerous online platforms and resources that offer interactive tutorials, practice problems, and step-by-step solutions. These resources provide a valuable supplement to traditional learning, allowing students to explore and master secant antiderivatives at their own pace.</p>
</div>
</div>
</div>
By delving into the intricacies of the secant antiderivative, we’ve gained a deeper understanding of this mathematical concept. With its practical applications and evolving role in various fields, the secant antiderivative remains a fascinating and essential tool in the realm of calculus.



