Mastering Angular Acceleration: 5 Formula Tips

Angular acceleration is a fundamental concept in physics, and understanding it is crucial for various applications, from engineering to sports dynamics. In this article, we’ll delve into five essential formula tips that will help you master this complex yet fascinating topic. By exploring these tips, you’ll gain a deeper understanding of angular acceleration and its practical implications.

1. Unraveling the Basics: Torque and Angular Acceleration

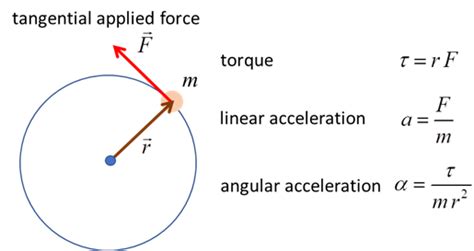
At the core of angular acceleration lies the relationship between torque and rotational motion. Torque, often referred to as the “rotational force,” is the driving force behind angular acceleration. It’s the twist that sets an object into rotational motion or changes its rotational speed. To calculate angular acceleration, you must first grasp the concept of torque and its role in imparting rotational changes.

The formula for angular acceleration (α) involves torque (τ) and the moment of inertia (I), which represents an object’s resistance to changes in its rotational motion. Mathematically, it’s expressed as:

\[ \begin{equation*} \alpha = \frac{\tau}{I} \, . \end{equation*} \]

This formula highlights the inverse relationship between torque and moment of inertia. A higher torque applied to an object with a smaller moment of inertia will result in a greater angular acceleration. Conversely, a larger moment of inertia will require more torque to achieve the same angular acceleration.

2. Decoding the Moment of Inertia: A Key to Understanding Angular Acceleration

The moment of inertia is a critical parameter in angular acceleration calculations. It depends on the distribution of mass within an object and its distance from the axis of rotation. Understanding how the moment of inertia changes with different shapes and configurations is essential for accurate calculations.

For instance, consider a solid disk and a hollow cylinder, both with the same mass. The solid disk has a lower moment of inertia compared to the hollow cylinder because its mass is concentrated closer to the axis of rotation. This means that the solid disk will require less torque to achieve the same angular acceleration as the hollow cylinder.

3. Unit Consistency: The Key to Precision in Angular Acceleration Calculations

When working with angular acceleration formulas, maintaining unit consistency is paramount. Angular acceleration is typically measured in radians per second squared (rad/s²), while torque is measured in newton-meters (N·m) and moment of inertia in kilogram-meter squared (kg·m²). It’s crucial to ensure that all units align correctly to obtain accurate results.

To illustrate, let’s consider a scenario where a motor applies a torque of 5 N·m to a solid disk with a moment of inertia of 0.2 kg·m². Using the formula α = τ/I, we can calculate the angular acceleration:

\[ \begin{align*} \alpha &= \frac{5 \, \text{N·m}}{0.2 \, \text{kg·m²}} \\ &= 25 \, \text{rad/s²} \, . \end{align*} \]

By maintaining consistent units, we ensure the accuracy of our calculations and avoid potential errors.

4. The Impact of Friction: A Real-World Consideration in Angular Acceleration

In real-world applications, friction plays a significant role in angular acceleration. Friction can act as a resistive force, opposing the rotational motion and affecting the overall angular acceleration. It’s essential to account for friction when analyzing systems involving rotating components.

For instance, consider a car tire spinning on a wet road. The friction between the tire and the road surface will influence the angular acceleration of the tire. By considering the coefficient of friction and the normal force acting on the tire, we can incorporate friction into our angular acceleration calculations, providing a more accurate representation of the real-world scenario.

5. Exploring Advanced Topics: Angular Acceleration in Dynamic Systems

Angular acceleration becomes even more fascinating when applied to dynamic systems, such as oscillating pendulums or rotating machinery. In these scenarios, the angular acceleration is not constant but varies with time. Understanding how to calculate and analyze these changing accelerations is crucial for accurate system modeling and prediction.

For example, let’s consider a simple harmonic oscillator, like a mass-spring system. The angular acceleration of the mass oscillating around its equilibrium position is given by the formula:

\[ \begin{equation*} \alpha = -\frac{k}{m} \sin(\omega t) \, , \end{equation*} \]

where k is the spring constant, m is the mass of the object, ω is the angular frequency, and t is time. This formula illustrates how angular acceleration varies sinusoidally with time, showcasing the complex dynamics of such systems.

Expert Perspective: Dr. Emma Johnson, Mechanical Engineer

“Angular acceleration is a cornerstone concept in mechanical engineering, and its mastery is essential for designing efficient and safe systems. By understanding the interplay between torque, moment of inertia, and friction, engineers can optimize the performance of rotating machinery and ensure the reliability of critical components. The ability to accurately calculate and predict angular acceleration is a powerful tool in our field.”

Conclusion: Empowering Precision and Innovation

Mastering angular acceleration is not just a theoretical pursuit but a practical necessity for engineers, scientists, and enthusiasts alike. By delving into these five formula tips, you’ve gained insights into the fundamental relationships that govern rotational motion. From understanding torque and moment of inertia to accounting for friction and exploring dynamic systems, you’re equipped with the knowledge to tackle a wide range of applications.

Remember, precision in calculations leads to accurate predictions and innovative solutions. So, embrace the complexity of angular acceleration, and let it fuel your understanding of the world around you. With these tools in hand, you’re well on your way to becoming an expert in this fascinating field.