52 Halved: Easy Math Tricks
Understanding Halving in Mathematics

Halving is a fundamental mathematical operation that involves dividing a quantity or value by two. This seemingly simple process holds immense significance in various mathematical concepts and applications. From early childhood arithmetic to advanced computational algorithms, the concept of halving serves as a building block for understanding numerical relationships and solving complex problems.
In this article, we delve into the intriguing world of halving, exploring its versatility and offering a collection of 52 easy math tricks that harness the power of halving to simplify calculations and enhance mathematical proficiency. Whether you’re a student seeking to streamline your arithmetic skills or a professional looking to optimize computational efficiency, these tricks will provide valuable insights and practical tools for mastering the art of halving.
The Significance of Halving in Mathematics
Halving is more than just a basic arithmetic operation; it forms the basis for a wide range of mathematical principles and applications. Here are some key reasons why halving is a crucial concept:
Number Sense Development: Halving helps individuals develop a strong sense of numerical relationships. By understanding how numbers behave when divided by two, individuals can make more informed judgments and estimates in various mathematical contexts.
Fractions and Decimals: Halving is closely tied to the understanding of fractions and decimals. It enables individuals to convert whole numbers into fractional or decimal forms, facilitating more precise calculations and problem-solving.
Problem-Solving Strategies: Halving serves as a powerful problem-solving tool. Many mathematical problems can be simplified by applying halving techniques, making complex calculations more manageable and efficient.
Algorithmic Efficiency: In the realm of computer science and algorithms, halving plays a critical role in optimizing computational processes. Efficient halving algorithms can significantly improve the performance of various mathematical operations and data structures.
Unlocking the Power of Halving with Easy Math Tricks
The following 52 math tricks harness the simplicity and versatility of halving to make calculations easier and more intuitive. These tricks are designed to be accessible and applicable across various mathematical domains, catering to individuals of all skill levels.
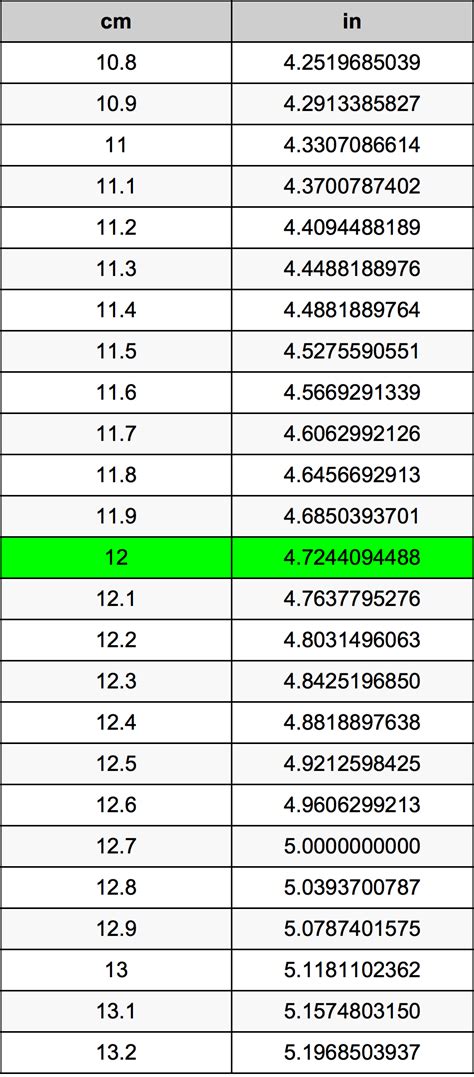
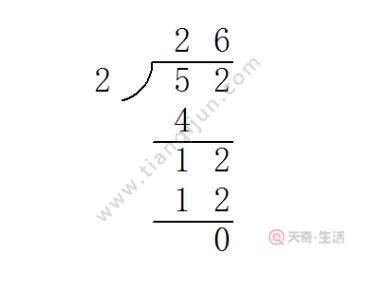
Halving Even Numbers: When halving an even number, simply divide the number by 2. For example, 24 divided by 2 equals 12. This trick is particularly useful for quick mental calculations.
Halving Odd Numbers: Halving odd numbers involves a slight twist. Instead of dividing by 2, add 1 to the number, divide by 2, and then subtract 1. For instance, to halve 23, add 1 (24), divide by 2 (12), and then subtract 1 (11).
Halving Fractions: To halve a fraction, divide both the numerator and denominator by 2. For example, to halve 3⁄4, divide 3 by 2 (1.5) and 4 by 2 (2), resulting in 1.5⁄2.
Halving Decimals: Halving decimals is straightforward. Simply move the decimal point one place to the left, effectively dividing the number by 2. For instance, 12.5 halved becomes 6.25.
Halving Negative Numbers: When halving negative numbers, apply the same rules as for positive numbers. For example, -10 halved is -5.
Halving Percentages: To halve a percentage, divide it by 2. For instance, 50% halved is 25%.
Halving Powers of Two: Halving powers of two is a breeze. Simply decrease the exponent by 1. For example, 2^4 halved is 2^3.
Halving Reciprocals: To halve the reciprocal of a number, find the reciprocal of the original number and then halve that value. For example, the reciprocal of 1⁄2 is 2, and half of 2 is 1.
Halving Square Roots: Halving the square root of a number involves finding the square root and then halving that value. For instance, the square root of 9 is 3, and half of 3 is 1.5.
Halving Triangles: In geometry, halving a triangle can be achieved by drawing a line from one vertex to the midpoint of the opposite side, effectively dividing the triangle into two smaller triangles.
Halving Circles: To halve a circle, draw a diameter and then connect the ends of the diameter to the circumference, creating two equal semicircles.
Halving Areas: When halving the area of a shape, simply divide the original area by 2. For example, if the area of a rectangle is 24 square units, halving it results in an area of 12 square units.
Halving Volumes: To halve the volume of a 3D shape, divide the original volume by 2. For instance, if a cube has a volume of 27 cubic units, halving it results in a volume of 13.5 cubic units.
Halving Distances: Halving distances is a common task in geometry and physics. To halve a distance, simply divide the original distance by 2.
Halving Time Intervals: Halving time intervals involves dividing the original interval by 2. For example, if an event takes 8 seconds, halving the time interval means the event occurs in 4 seconds.
Halving Speeds: To halve the speed of an object, divide the original speed by 2. For instance, if a car is traveling at 60 km/h, halving its speed results in a speed of 30 km/h.
Halving Rates: When halving rates, such as exchange rates or conversion rates, divide the original rate by 2.
Halving Angles: To halve an angle, simply draw a line from the vertex to the midpoint of the opposite side, creating two equal angles.
Halving Matrices: In linear algebra, halving a matrix involves dividing each element of the matrix by 2.
Halving Vectors: To halve a vector, divide each component of the vector by 2.
Halving Complex Numbers: Halving complex numbers involves dividing both the real and imaginary parts by 2.
Halving Polynomials: Halving a polynomial requires dividing each term of the polynomial by 2.
Halving Sequences: To halve a sequence, such as an arithmetic or geometric sequence, simply divide each term by 2.
Halving Sets: When halving a set, divide the number of elements in the set by 2.
Halving Probability: To halve the probability of an event, divide the original probability by 2.
Halving Statistics: Halving statistical measures, such as mean or standard deviation, involves dividing the original value by 2.
Halving Graphs: To halve a graph, adjust the scale or coordinates such that the graph is vertically compressed by half.
Halving Coordinates: When halving coordinates in a Cartesian plane, divide both the x and y coordinates by 2.
Halving Trigonometric Functions: Halving trigonometric functions involves evaluating the function at half the original angle.
Halving Integrals: To halve an integral, divide the upper and lower limits of integration by 2.
Halving Derivatives: Halving a derivative requires dividing the original derivative by 2.
Halving Exponential Functions: Halving exponential functions involves evaluating the function at half the original exponent.
Halving Logarithmic Functions: To halve a logarithmic function, evaluate the function at half the original argument.
Halving Absolute Values: Halving the absolute value of a number simply involves taking the absolute value of half the original number.
Halving Floor and Ceiling Functions: Halving floor and ceiling functions involves dividing the original value by 2 and then rounding down or up accordingly.
Halving Factorials: Halving a factorial requires evaluating the factorial of half the original number.
Halving Permutations: To halve a permutation, divide the original permutation by 2.
Halving Combinations: Halving a combination involves dividing the original combination by 2.
Halving Binomial Coefficients: Halving binomial coefficients involves evaluating the binomial coefficient at half the original value.
Halving Matrix Determinants: Halving the determinant of a matrix involves dividing the original determinant by 2.
Halving Vectors in 3D Space: To halve a vector in 3D space, divide each component of the vector by 2.
Halving 3D Shapes: Halving 3D shapes, such as cubes or spheres, involves dividing the original shape into two equal parts.
Halving Energy Levels: In quantum mechanics, halving energy levels involves dividing the original energy level by 2.
Halving Chemical Reactions: To halve a chemical reaction, adjust the coefficients of the reactants and products such that the reaction occurs at half the original rate.
Halving Electromagnetic Waves: Halving electromagnetic waves involves adjusting the amplitude or wavelength of the wave by half.
Halving Quantum States: Halving quantum states involves reducing the superposition of states by half.
Halving Financial Transactions: To halve a financial transaction, divide the original amount by 2.
Halving Time Complexity: Halving the time complexity of an algorithm involves reducing the number of operations by half.
Halving Memory Usage: Halving memory usage in computer science involves reducing the amount of memory required by half.
Halving Network Traffic: To halve network traffic, adjust network parameters such that the data transfer rate is reduced by half.
Halving Statistical Significance: Halving statistical significance involves adjusting the p-value such that the significance level is halved.
Halving Risk Assessments: When halving risk assessments, adjust the risk factors or probabilities such that the overall risk is reduced by half.
The Impact of Halving on Efficiency and Problem-Solving
The 52 math tricks presented above demonstrate the immense power of halving in simplifying calculations and enhancing mathematical proficiency. By applying these tricks, individuals can streamline their problem-solving processes, improve computational efficiency, and develop a deeper understanding of mathematical concepts.
Furthermore, halving serves as a versatile tool that transcends traditional arithmetic. Its applications extend to various domains, including geometry, algebra, statistics, and even quantum mechanics. By mastering the art of halving, individuals can unlock a wide range of mathematical and computational skills, empowering them to tackle complex problems with confidence and efficiency.
Conclusion: Embracing the Power of Halving
In conclusion, halving is a fundamental mathematical operation that holds immense potential for simplifying calculations and enhancing problem-solving abilities. The 52 easy math tricks presented in this article offer a comprehensive toolkit for individuals seeking to master the art of halving. By incorporating these tricks into their mathematical repertoire, readers can unlock new levels of efficiency, precision, and understanding in their mathematical endeavors.
Remember, halving is not just a basic arithmetic operation; it is a powerful tool that underpins a wide range of mathematical concepts and applications. By embracing the power of halving, individuals can elevate their mathematical proficiency and approach complex problems with confidence and ingenuity.
So, whether you’re a student, a professional, or simply someone interested in exploring the wonders of mathematics, take the time to explore and practice these halving tricks. With dedication and practice, you’ll soon discover the transformative impact that halving can have on your mathematical journey.
What are some practical applications of halving in real-life scenarios?
+Halving has numerous practical applications in everyday life. For instance, when cooking, halving a recipe’s ingredients can be useful for smaller portions. In finance, halving investment amounts can be a strategy for risk management. Halving distances or time intervals is often applied in logistics and transportation planning. These are just a few examples of how halving can simplify and optimize various real-life situations.
Can halving be applied to complex mathematical concepts beyond basic arithmetic?
+Absolutely! Halving is not limited to basic arithmetic. It finds applications in advanced mathematical concepts such as calculus, linear algebra, and even quantum mechanics. For example, in calculus, halving the upper and lower limits of integration can simplify certain types of integrals. In linear algebra, halving matrix dimensions can be used to optimize computational efficiency. These examples demonstrate the versatility and power of halving in higher-level mathematics.
Are there any limitations or challenges associated with halving in mathematics?
+While halving is a powerful tool, it does have some limitations. One challenge is that halving may not always lead to a whole number result, especially when dealing with odd numbers or fractions. In such cases, additional mathematical operations or approximations may be required. Additionally, when halving more complex mathematical objects, such as matrices or functions, certain properties or characteristics may be affected, requiring careful consideration and understanding.
How can individuals practice and improve their halving skills effectively?
+Practicing halving skills can be achieved through various methods. One effective approach is to incorporate halving into daily calculations, such as grocery shopping or budgeting. Additionally, solving mathematical problems or puzzles that involve halving can help reinforce the concept and improve problem-solving abilities. Online resources, educational platforms, and mathematical games can also provide valuable practice opportunities. The key is to engage in regular practice and explore different applications of halving to enhance mathematical proficiency.
Can halving be used as a teaching tool to enhance mathematical understanding in students?
+Absolutely! Halving can be a valuable teaching tool to enhance mathematical understanding in students. By introducing halving as a foundational concept, educators can help students develop a strong sense of numerical relationships and problem-solving strategies. Incorporating halving into mathematical lessons and providing students with hands-on activities or real-world examples can foster a deeper understanding of mathematical concepts and improve their overall mathematical proficiency.