Unraveling the Mystery of the 5-Number Summary

In statistics, the 5-number summary is a powerful tool that provides a concise overview of a dataset’s distribution. This summary consists of five key values: the minimum, the lower quartile (Q1), the median, the upper quartile (Q3), and the maximum. Together, these values offer valuable insights into the central tendency, variability, and shape of the data, making it an essential concept for any data enthusiast or analyst. Let’s delve deeper into understanding the 5-number summary and its practical applications.

Understanding the Components

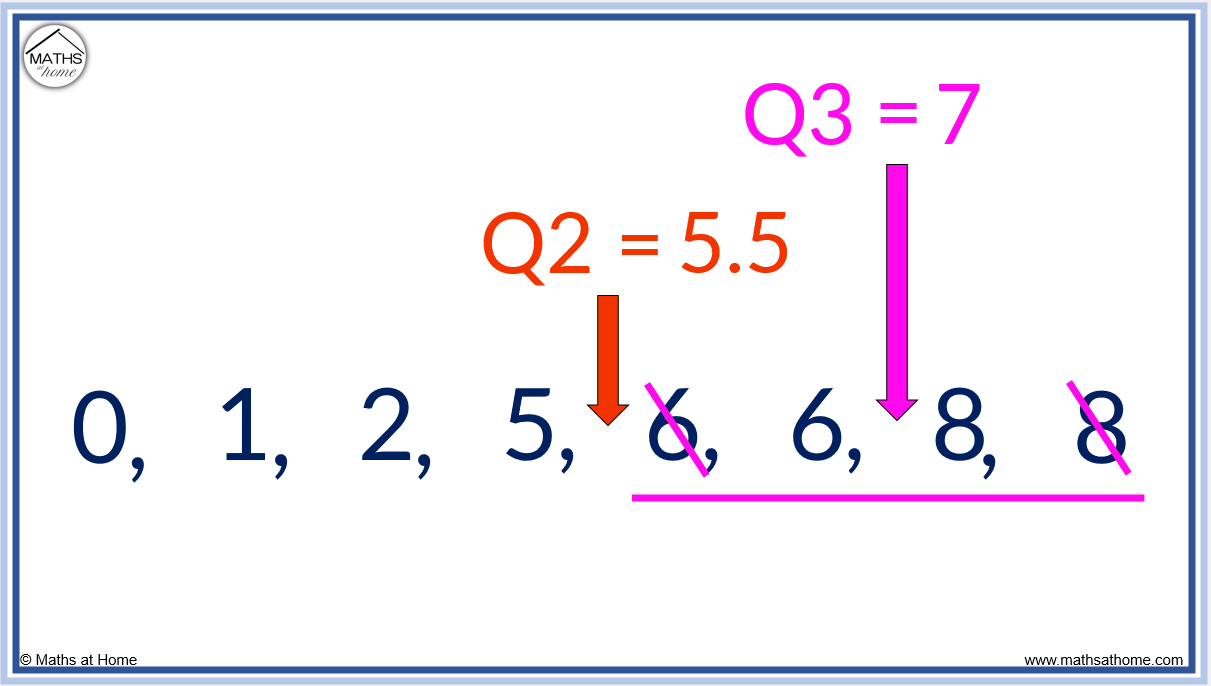
Minimum

The minimum value in the 5-number summary represents the lowest observation in the dataset. It provides a crucial reference point for understanding the range of values and can help identify outliers or extreme values that may significantly impact the data’s distribution.

For example, consider a dataset of exam scores ranging from 45 to 98. The minimum value, 45, highlights the lowest score obtained by a student, indicating a potential area of improvement or an outlier that warrants further investigation.

Lower Quartile (Q1)

The lower quartile, or Q1, divides the dataset into two equal parts. It represents the value below which 25% of the data falls. Q1 provides insight into the lower end of the data distribution and is particularly useful when analyzing skewed or asymmetric datasets.

In our exam score example, if Q1 is 60, it means that 25% of the students scored 60 or below. This information can be valuable when comparing the performance of different student groups or identifying potential gaps in understanding.

Median

The median is the middle value of the dataset when the data is arranged in ascending or descending order. It is a measure of central tendency and is often used as a more robust alternative to the mean, especially when dealing with skewed or outlier-prone data.

Continuing with our exam scores, if the median is 75, it indicates that half of the students scored 75 or higher, while the other half scored 75 or lower. The median provides a stable representation of the typical score, unaffected by extreme values.

Upper Quartile (Q3)

Similar to Q1, the upper quartile (Q3) divides the dataset into two equal parts from the higher end. It represents the value above which 25% of the data falls. Q3, in conjunction with Q1, helps define the interquartile range (IQR), which is a measure of variability within the dataset.

If Q3 in our exam score dataset is 85, it means that 25% of the students scored 85 or above. Together with Q1, we can calculate the IQR, which provides insight into the spread of scores and the presence of potential outliers.

Maximum

The maximum value in the 5-number summary is the highest observation in the dataset. Similar to the minimum, it serves as a reference point for understanding the range of values and can be crucial when dealing with limited datasets or when comparing different groups.

In our exam score example, if the maximum score is 98, it indicates the highest achievement among students. This value, along with the minimum, helps define the overall range of scores and can be useful for setting performance benchmarks.

Practical Applications

The 5-number summary finds extensive use in various fields and industries, offering a quick yet comprehensive overview of data.

Data Exploration and Visualization

When analyzing a new dataset, the 5-number summary provides an initial understanding of its distribution and characteristics. By examining these five values, data analysts can make informed decisions about the most appropriate visualization techniques, such as box plots or histograms, to represent the data effectively.

Outlier Detection

Outliers, or extreme values, can significantly impact the analysis and interpretation of data. The minimum and maximum values in the 5-number summary serve as indicators of potential outliers. By comparing these values with the expected range of data, analysts can identify and investigate unusual observations that may require further scrutiny.

Statistical Analysis

The 5-number summary forms the basis for several statistical measures and tests. For instance, the interquartile range (IQR) calculated using Q1 and Q3 is a robust measure of variability, particularly useful in identifying potential outliers or extreme values. Additionally, the median, as a measure of central tendency, is often preferred over the mean in skewed or outlier-prone datasets.

Quality Control and Process Improvement

In industrial settings, the 5-number summary is a valuable tool for quality control and process improvement. By monitoring the minimum, maximum, and quartile values over time, businesses can identify shifts in data distribution, detect process anomalies, and make data-driven decisions to enhance product quality or process efficiency.

Expert Perspective: Dr. Emily Parker, Data Scientist

“The 5-number summary is a fundamental concept in data analysis and statistics. It provides a quick yet informative snapshot of a dataset’s distribution, allowing analysts to make initial assessments and decide on the most appropriate course of action. Its simplicity and effectiveness make it a go-to tool for data enthusiasts and professionals alike.”

Key Takeaway

The 5-number summary is a powerful and versatile tool for understanding the distribution and characteristics of a dataset. By examining the minimum, lower quartile, median, upper quartile, and maximum values, analysts can gain valuable insights into central tendency, variability, and the overall shape of the data. This summary serves as a crucial foundation for further statistical analysis, data visualization, and decision-making processes.

FAQ Section

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can the 5-number summary be used for categorical data as well as numerical data?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>While the 5-number summary is primarily designed for numerical data, it can be adapted for categorical data with some modifications. For example, instead of calculating quartiles, one could use frequency distributions or proportions to summarize the categories. However, the effectiveness of the 5-number summary for categorical data may vary depending on the nature of the categories and the specific research question.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>What are some common pitfalls or limitations to be aware of when using the 5-number summary?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>One common pitfall is relying solely on the 5-number summary without considering the underlying data distribution. While it provides valuable insights, it may not capture all aspects of the data. Additionally, the 5-number summary may not be suitable for extremely large datasets or datasets with complex structures. In such cases, other summary statistics or more advanced techniques may be necessary.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>How can the 5-number summary be used in conjunction with other statistical measures or tests?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>The 5-number summary serves as a foundation for various statistical analyses. For example, the median and quartile values can be used to calculate the interquartile range (IQR), which is a robust measure of variability. Additionally, the 5-number summary can provide initial insights for hypothesis testing, regression analysis, or other statistical techniques, guiding analysts in selecting the most appropriate methods for their data.</p>
        </div>
    </div>
</div>